Which expression is a factor of x^2 + 7x - 30?
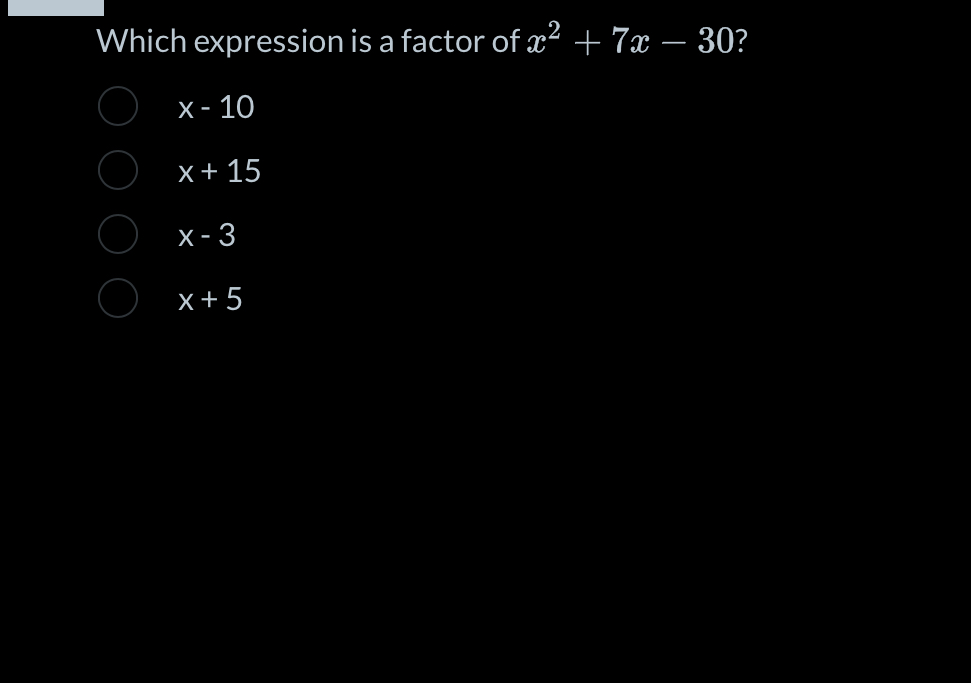
Understand the Problem
The question asks to identify which of the provided expressions is a factor of the quadratic expression (x^2 + 7x - 30). To determine the correct factor, we need to factor the quadratic expression and see which of the options matches one of the factors.
Answer
$x-3$
Answer for screen readers
$x-3$
Steps to Solve
- Factor the quadratic expression
We are given the quadratic expression $x^2 + 7x - 30$. We need to find two numbers that multiply to -30 and add to 7.
- Identify the two numbers
The numbers 10 and -3 satisfy these conditions, since $10 \times -3 = -30$ and $10 + (-3) = 7$.
- Rewrite the quadratic expression in factored form
Using the numbers 10 and -3, we can rewrite the quadratic expression in factored form as $(x + 10)(x - 3)$.
- Identify the factor from the options
Now we check the options provided to see which one matches one of the factors we found. We have the factors $(x+10)$ and $(x-3)$. The option $x-3$ matches one of the factors.
$x-3$
More Information
The factored form of $x^2 + 7x - 30$ is indeed $(x+10)(x-3)$. Therefore, $x-3$ and $x+10$ are both factors of the given quadratic expression.
Tips
A common mistake is to incorrectly identify the two numbers that multiply to -30 and add to 7. For example, one might choose -10 and 3, which add to -7 instead of 7. Another common mistake is to forget the signs of the numbers during factorization, leading to an incorrect factored form.
AI-generated content may contain errors. Please verify critical information