Which expression does not belong with the other three? Explain your reasoning.
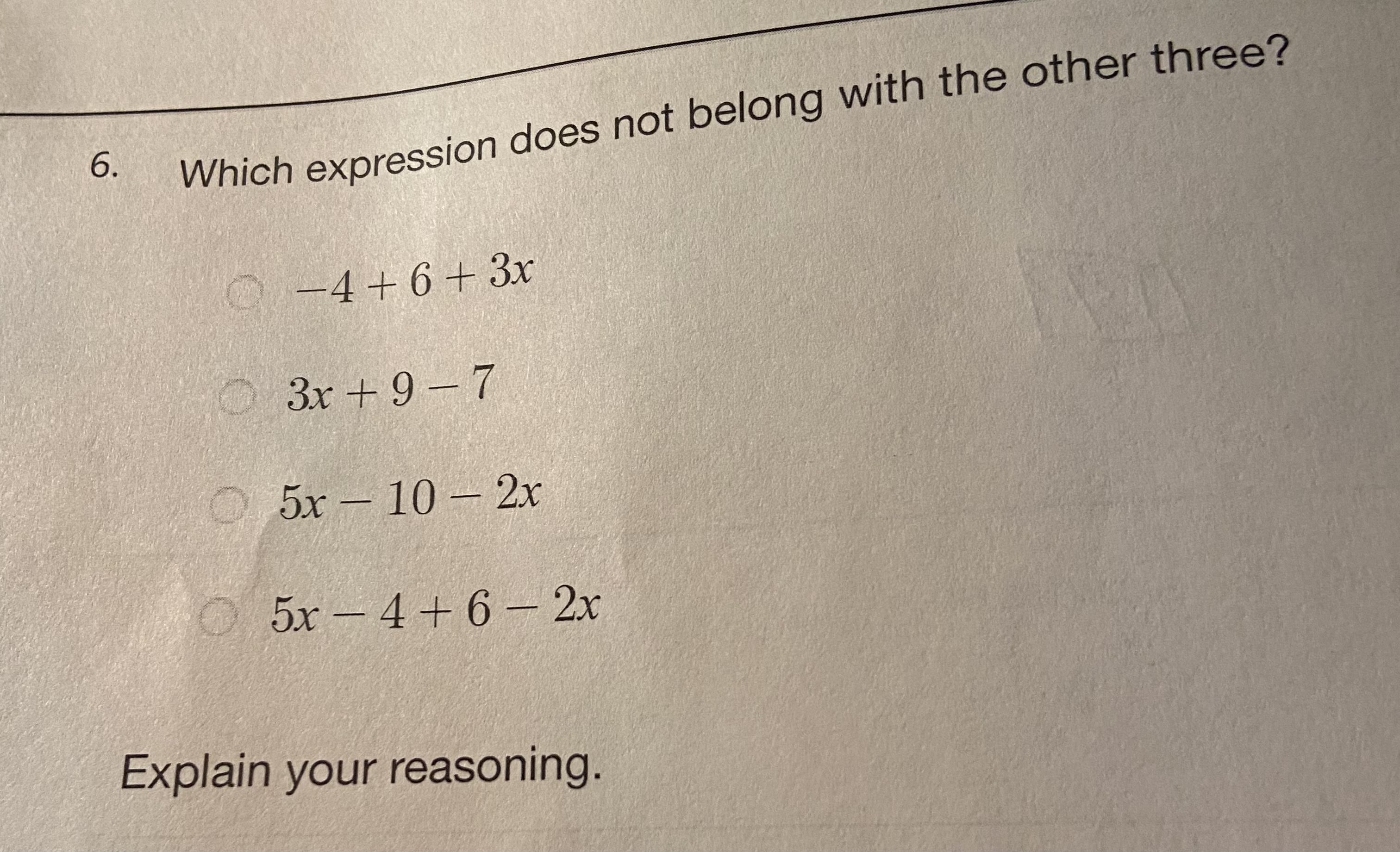
Understand the Problem
The question is asking to identify which of the provided expressions does not belong with the others based on a particular property, likely related to algebraic expressions or their forms. The user is also asked to explain their reasoning for this choice.
Answer
The expression that does not belong is $5x - 10 - 2x$.
Answer for screen readers
The expression that does not belong is $5x - 10 - 2x$.
Steps to Solve
- Identify the Expressions The given expressions are:
- $-4 + 6 + 3x$
- $3x + 9 - 7$
- $5x - 10 - 2x$
- $5x - 4 + 6 - 2x$
- Simplify Each Expression We simplify each expression to examine their forms.
-
For $-4 + 6 + 3x$: $$ -4 + 6 = 2 \quad \Rightarrow \quad 2 + 3x = 3x + 2 $$
-
For $3x + 9 - 7$: $$ 9 - 7 = 2 \quad \Rightarrow \quad 3x + 2 $$
-
For $5x - 10 - 2x$: $$ 5x - 2x - 10 = 3x - 10 $$
-
For $5x - 4 + 6 - 2x$: $$ -4 + 6 = 2 \quad \Rightarrow \quad 5x - 2x + 2 = 3x + 2 $$
- Compare the Simplified Forms Comparing the simplified forms obtained:
- First two expressions simplify to $3x + 2$.
- The third expression simplifies to $3x - 10$.
- The last expression simplifies to $3x + 2$.
- Identify the Odd Expression The expression that is different is $5x - 10 - 2x$, which simplifies to $3x - 10$.
The expression that does not belong is $5x - 10 - 2x$.
More Information
This expression is distinct because it has a different constant term compared to the others, which all simplify to $3x + 2$. Recognizing the significance of constant terms is crucial when comparing algebraic expressions.
Tips
- Failing to simplify all expressions before comparing them can lead to incorrect conclusions.
- Not accurately combining like terms, especially in expressions with both constants and variables.
