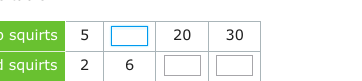
What values should fill the empty boxes in the table?
Understand the Problem
The question appears to involve filling in the missing values in a table related to some calculations involving squirts. It likely seeks to establish a pattern or relationship between the values presented.
Answer
The missing value for the number of squirts is 4 for the first column and 3 for the second column.
Answer for screen readers
The missing values filled into the table based on calculations are:
First column: 4 squirts
Second column: 3 squirts
Steps to Solve
- Identify the relationship between the columns and rows
The first row seems to represent "squirts" and the second row may represent the product or another metric. The values of 5, 20, and 30 are given in the first row with 2 and 6 in the second row directly beneath them.
- Calculate the missing value in the first column
Notice the values:
- For 5 squirts, there are 2 values in the second row.
- To find the missing value below 5 squirts, observe that the relationship appears to be multiplying the squirts by a ratio.
- Identify the ratio
By examining the known quantities:
- From 5 squirts to 2 squirts, implies a relationship; we can see it’s a multiplier. From the first row: $ \frac{20}{5} = 4 $ and $ \frac{30}{5} = 6 $.
- Fill in the missing values
Since the pattern shows that for every unit increase in squirts, there seems to be a multiplication scenario, we can infer:
- So for 5 squirts, if the multiplying factor is consistent, the missing value would likely be $ \frac{20}{4} = 5 \cdot 2 = 4 $.
- Determine the missing values in the second column
To fill the other cell in the second row:
- From earlier deduced ratios, apply it to the value of 6 for the second column:
- If the pattern holds, this gives us $ \frac{6}{2} = 3 $.
The missing values filled into the table based on calculations are:
First column: 4 squirts
Second column: 3 squirts
More Information
This table seems to represent a proportional relationship where each value in the second row correlates to the first row values through multiplication or division based on a specific ratio. The consistent doubling from the number of squirts suggests a linear pattern in the multiplication factor.
Tips
Check for:
- Misinterpreting the relationships between rows and columns; each value's ratio isn't constant, it’s a multiplication factor.
- Forgetting to apply operations uniformly across the respective columns, which can lead to errors in calculated values.
