What value of p makes the equation true? 7(p + 1) = 9 + 6p
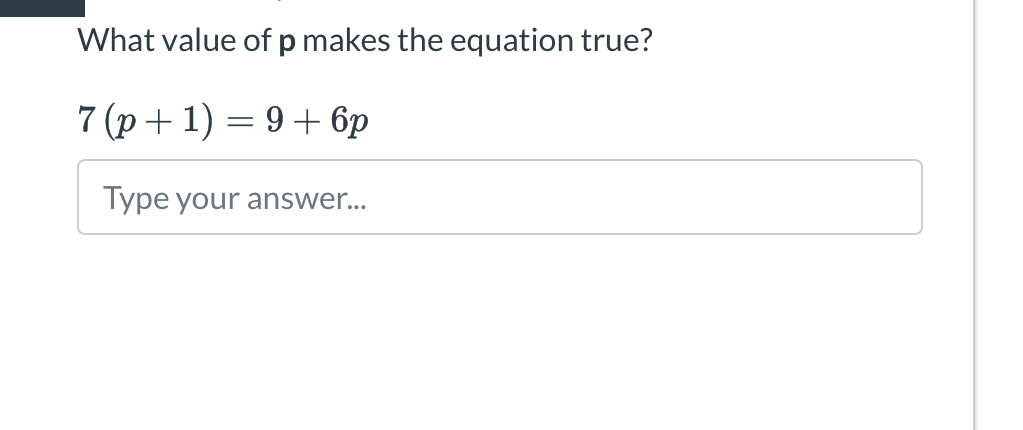
Understand the Problem
The question is asking for the value of p that satisfies the equation 7(p + 1) = 9 + 6p. We will solve this equation step by step to find the value of p.
Answer
The value of $p$ is \( p = 2 \).
Answer for screen readers
The value of $p$ that makes the equation true is ( p = 2 ).
Steps to Solve
-
Distribute the 7 on the left side
We start by distributing the 7 in the equation:
$$ 7(p + 1) = 9 + 6p $$
becomes
$$ 7p + 7 = 9 + 6p $$
-
Get all terms involving p on one side
Next, we want to isolate the variable $p$. We'll subtract $6p$ from both sides:
$$ 7p + 7 - 6p = 9 + 6p - 6p $$
which simplifies to
$$ p + 7 = 9 $$
-
Isolate p by subtracting 7 from both sides
Now we will subtract 7 from both sides of the equation:
$$ p + 7 - 7 = 9 - 7 $$
This gives us
$$ p = 2 $$
The value of $p$ that makes the equation true is ( p = 2 ).
More Information
This equation was solved using basic algebraic principles, including distribution and moving terms across the equality. The solution indicates where $p$ equals 2 makes both sides of the original equation equal.
Tips
- Not distributing properly: Sometimes, students forget to distribute the number across the parentheses. Always check that each term is accounted for.
- Rearranging incorrectly: Ensure that when moving variables across the equal sign, the operations performed are correct (e.g., if you subtract, ensure to subtract from both sides).
AI-generated content may contain errors. Please verify critical information