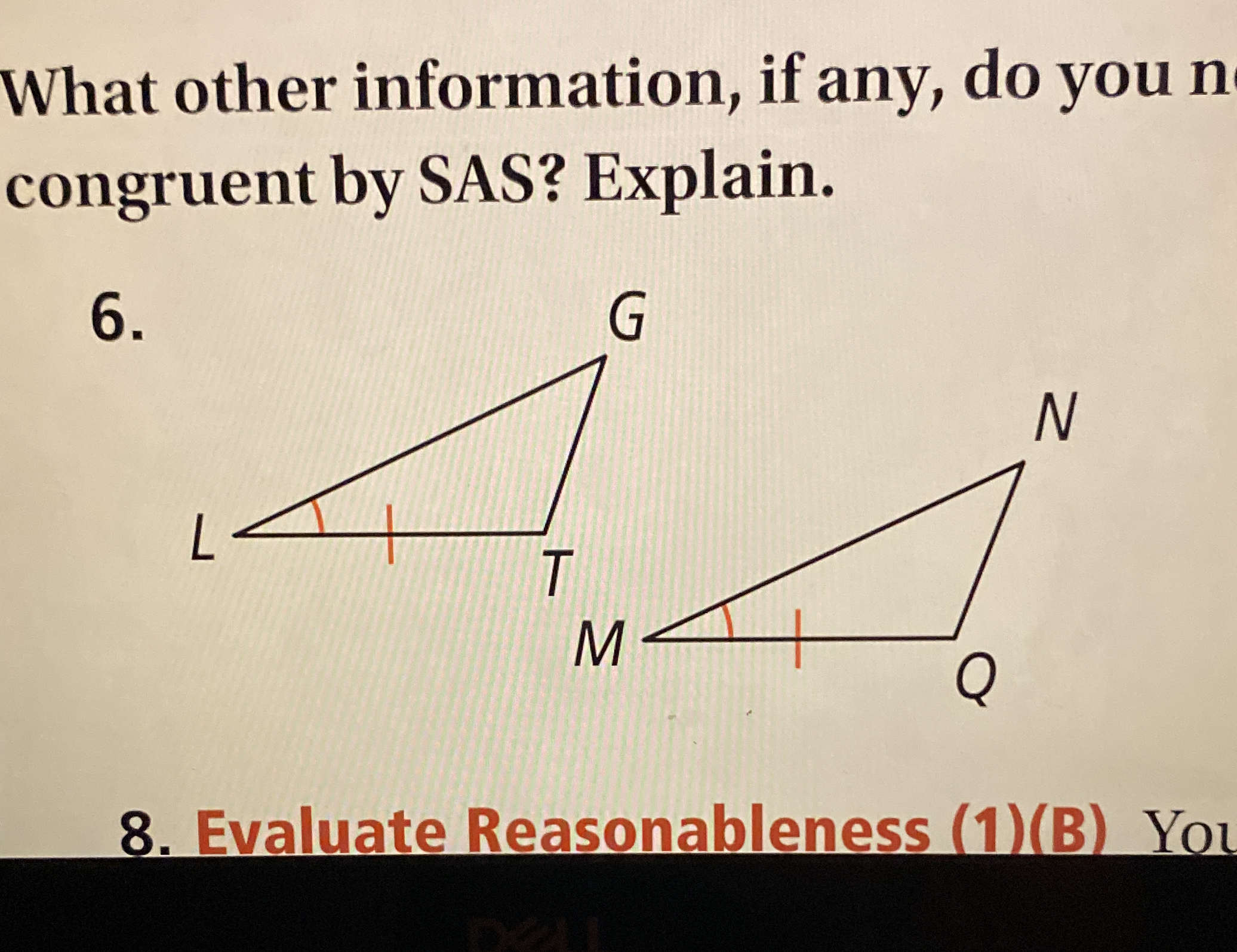
What other information, if any, do you need for the triangles to be congruent by SAS? Explain.
Understand the Problem
The question is asking for additional information needed to prove that two triangles are congruent using the Side-Angle-Side (SAS) congruence criterion. It also requires an explanation of the reasoning behind this.
Answer
We need the length of \( LT \) or \( GQ \) for congruence by SAS, plus confirmation of equal included angles.
Answer for screen readers
We need the length of ( LT ) or ( GQ ) to determine congruence, plus confirmation that the included angles are equal.
Steps to Solve
-
Identify the Given Information We have two triangles, ( \triangle LTM ) and ( \triangle GQN ), which have one side and the included angle marked. Specifically, the segment ( LM ) is equal to ( GQ ), and the angles ( \angle LTM ) and ( \angle GQN ) are shown as equal (due to the given markings).
-
Applying the SAS Criterion For two triangles to be proven congruent by the Side-Angle-Side (SAS) criterion, we need two sides and the included angle of one triangle to be equal to the corresponding two sides and the included angle of the other triangle.
-
Identify Missing Information To apply the SAS criterion, we need to confirm that:
- The length of side ( LT ) is known or can be proven equal to side ( GQ ) (or another corresponding side).
- The included angle (the angle between the two given sides) must be the same for both triangles.
-
Conclusion Thus, to prove that the triangles are congruent by SAS, we need the length of another side and confirmation that the included angles are indeed equal.
We need the length of ( LT ) or ( GQ ) to determine congruence, plus confirmation that the included angles are equal.
More Information
The SAS criterion is a fundamental method in triangle congruence, where two sides and the included angle must be congruent to establish triangle equivalence. Understanding how triangles can be congruent through different criteria (like SSS, ASA, AAS) is crucial for further geometry studies.
Tips
- Assuming two angles are equal without proof can lead to incorrect conclusions about congruence.
- Not labeling or marking congruent sides and angles in diagrams may lead to oversight when applying congruence criteria.
AI-generated content may contain errors. Please verify critical information