What is the volume of this cone? Use $\pi \approx 3.14$ and round your answer to the nearest hundredth.
Understand the Problem
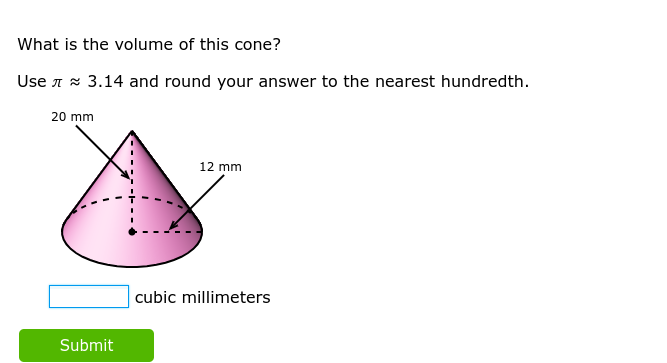
The question asks to find the volume of the cone, using the measurements provided. The image shows the radius is 12mm and the height is 20mm, use the formula $V = (1/3) * \pi * r^2 * h$ to solve, using $\pi=3.14$, and round to the nearest hundredth.
Answer
$3014.4$
Answer for screen readers
$3014.4$
Steps to Solve
- Write down the formula for the volume of a cone
The volume $V$ of a cone is given by the formula:
$$V = \frac{1}{3} \pi r^2 h$$
where $r$ is the radius and $h$ is the height.
- Plug in known values
We are given that $r = 12$ mm, $h = 20$ mm, and $\pi \approx 3.14$. Substituting these values into the formula, we get:
$$V = \frac{1}{3} \times 3.14 \times (12)^2 \times 20$$
- Calculate $r^2$
$$V = \frac{1}{3} \times 3.14 \times 144 \times 20$$
- Multiply values
Multiply $3.14 \times 144 \times 20$:
$$V = \frac{1}{3} \times 9043.2$$
- Divide by 3 Divide $9043.2$ by $3$:$$V = 3014.4$$
The volume of the cone is $3014.4$ cubic millimeters.
$3014.4$
More Information
The volume is in cubic millimeters because we are measuring the cone in three dimensions.
Tips
A common mistake is forgetting to square the radius in the formula. Another one is performing the operations in the wrong order. Also, forgetting to divide by 3.
AI-generated content may contain errors. Please verify critical information