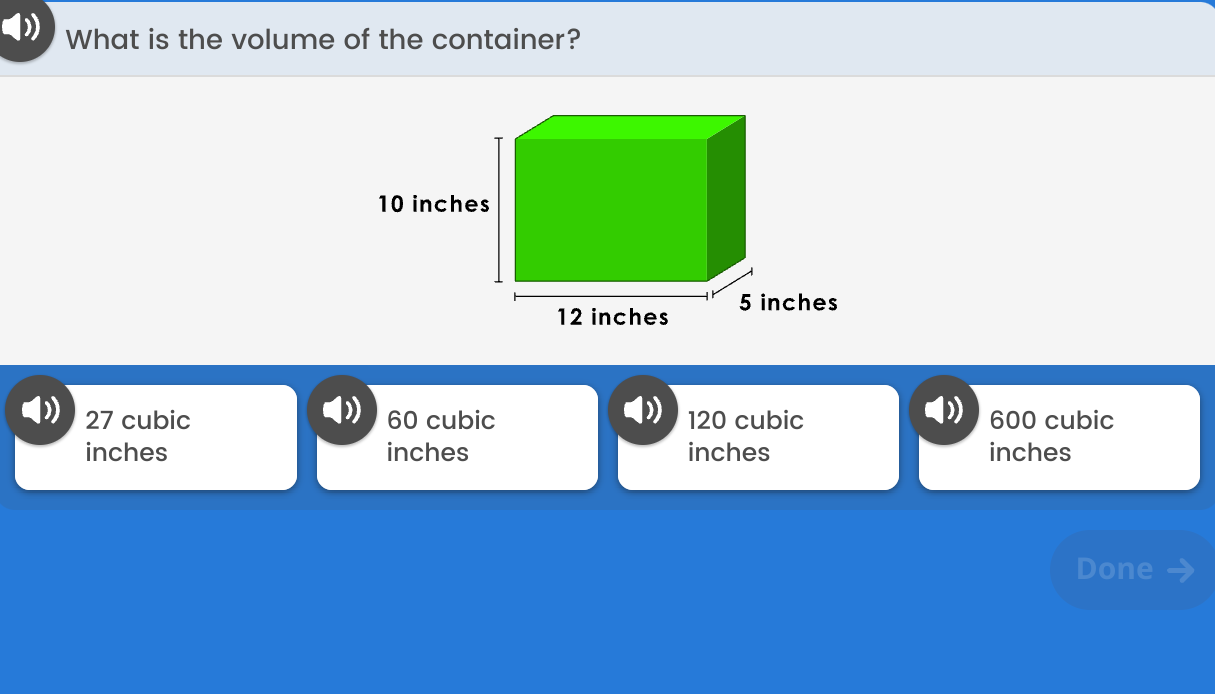
What is the volume of the container?
Understand the Problem
The question is asking for the volume of a rectangular container with given dimensions (length, width, and height). To find the volume, we will use the formula: Volume = length × width × height.
Answer
The volume of the container is \( 600 \, \text{cubic inches} \).
Answer for screen readers
The volume of the container is ( 600 , \text{cubic inches} ).
Steps to Solve
- Identify the dimensions of the container
The dimensions given are:
- Length = 12 inches
- Width = 5 inches
- Height = 10 inches
- Apply the volume formula
To find the volume of a rectangular container, use the formula:
$$ \text{Volume} = \text{length} \times \text{width} \times \text{height} $$
- Substitute the values into the formula
Substituting the identified dimensions into the volume formula:
$$ \text{Volume} = 12 , \text{inches} \times 5 , \text{inches} \times 10 , \text{inches} $$
- Calculate the volume
Now, perform the multiplication:
$$ \text{Volume} = 12 \times 5 \times 10 $$
Calculating step-by-step:
- First, calculate ( 12 \times 5 = 60 )
- Then, calculate ( 60 \times 10 = 600 )
Thus, the total volume is:
$$ \text{Volume} = 600 , \text{cubic inches} $$
The volume of the container is ( 600 , \text{cubic inches} ).
More Information
The volume of a rectangular container provides the amount of space it can hold. In this case, it can hold 600 cubic inches of liquid or any other substance.
Tips
- Failing to multiply all three dimensions together.
- Mixing up the dimensions (interchanging length, width, and height).
- Forgetting to use consistent units of measurement.
AI-generated content may contain errors. Please verify critical information