What is the voltage at R2?

Understand the Problem

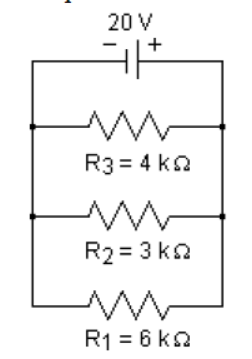
The question is asking for the voltage across resistor R2 in a circuit with three resistors connected in parallel to a 20V source. To solve this, we will calculate the total resistance of the parallel circuit and then use the voltage divider rule to find the voltage across R2.

Answer

The voltage across resistor $ R_2 $ is $ 20V $.

Steps to Solve

Calculate Total Resistance in Parallel

To find the total resistance ( R_t ) of resistors in parallel, use the formula: $$ \frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} $$ Substituting the values: $$ \frac{1}{R_t} = \frac{1}{6 , k\Omega} + \frac{1}{3 , k\Omega} + \frac{1}{4 , k\Omega} $$

Find the Total Resistance

Calculate the right side of the equation: $$ \frac{1}{R_t} = \frac{1}{6} + \frac{1}{3} + \frac{1}{4} $$ Finding a common denominator (12): $$ \frac{1}{R_t} = \frac{2}{12} + \frac{4}{12} + \frac{3}{12} = \frac{9}{12} = \frac{3}{4} $$ Thus, $$ R_t = \frac{4}{3} , k\Omega \approx 1.33 , k\Omega $$

Use the Voltage Divider Rule

Since all resistors are in parallel, the voltage across each resistor is equal to the source voltage. Therefore: $$ V_{R2} = V_{source} = 20V $$

Final Result

The voltage across resistor ( R_2 ) is: $$ V_{R2} = 20V $$

The voltage across resistor ( R_2 ) is ( 20V ).

More Information

In a parallel circuit, all components share the same voltage, which is equal to the voltage of the power source. This makes calculating the voltage across individual resistors straightforward, as they all experience the same voltage drop.

Tips

Confusing series and parallel circuits can lead to incorrect calculations. Remember that in parallel circuits, the voltage across each resistor is the same as the source voltage.
Forgetting to convert kΩ to Ω if needed for computations, though here it’s not necessary since the calculations are directly based on the resistors' kΩ values.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!