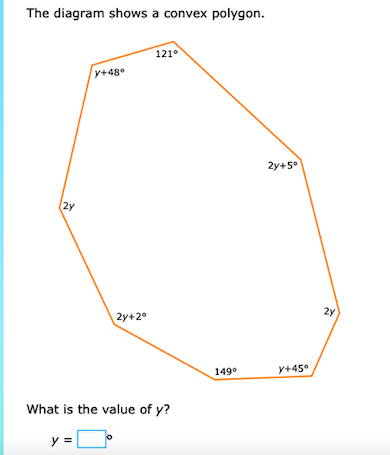
What is the value of y?
Understand the Problem
The question is asking us to find the value of y in a polygon where the angles are expressed in terms of y. We need to set up an equation based on the property that the sum of the interior angles of a polygon can be calculated and solve for y.
Answer
$y = 60$
Answer for screen readers
The value of $y$ is $60^\circ$.
Steps to Solve
- Determine the Number of Sides of the Polygon
Identify the angles provided, which are:
- $y + 48^\circ$
- $121^\circ$
- $2y + 5^\circ$
- $2y$
- $2y + 2^\circ$
- $149^\circ$
- $y + 45^\circ$
This polygon has 7 sides.
- Calculate the Sum of the Interior Angles
The formula for the sum of the interior angles of a polygon with $n$ sides is:
$$ \text{Sum of interior angles} = (n - 2) \times 180^\circ $$
Substituting $n = 7$:
$$ \text{Sum} = (7 - 2) \times 180 = 5 \times 180 = 900^\circ $$
- Set Up the Equation
Add up all the angles expressed in terms of $y$:
$$ (y + 48) + 121 + (2y + 5) + 2y + (2y + 2) + 149 + (y + 45) = 900 $$
- Combine Like Terms
Combine all terms involving $y$ and the constant terms:
$$ y + 2y + 2y + 2y + y + 48 + 121 + 5 + 2 + 149 + 45 = 900 $$ This simplifies to:
$$ 8y + 420 = 900 $$
- Isolate $y$
Subtract 420 from both sides:
$$ 8y = 900 - 420 $$ $$ 8y = 480 $$
- Solve for $y$
Divide both sides by 8:
$$ y = \frac{480}{8} $$ $$ y = 60 $$
The value of $y$ is $60^\circ$.
More Information
In a polygon with 7 sides, the sum of the interior angles is important for determining unknown angle measures. Here, we found $y$ by expressing all angles in terms of $y$ and solving the equation according to the properties of polygons.
Tips
- Not using the correct formula: Ensure the sum of the interior angles formula is correctly applied based on the number of sides.
- Incorrectly combining like terms: Be careful when adding terms; verify that all $y$ terms and constants are correctly tallied.
AI-generated content may contain errors. Please verify critical information