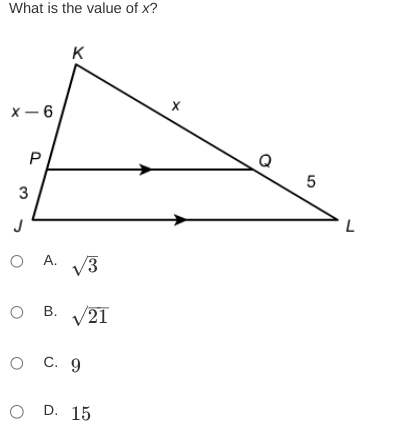
What is the value of x?

Steps to Solve

1. Identify the similar triangles

The triangle $\triangle KJP$ is similar to triangle $\triangle QJL$ because they share angle $J$ and have corresponding parallel sides $PK$ and $QL$. This means the ratios of the lengths of corresponding sides are equal.

2. Set up the proportion

Using the property of similar triangles, we can set up the following equation based on the corresponding sides:

$$ \frac{x - 6}{5} = \frac{3}{x} $$

3. Cross multiply

To eliminate the fractions, we can cross multiply:

$$ (x - 6) \cdot x = 5 \cdot 3 $$

This simplifies to:

$$ x^2 - 6x = 15 $$

4. Rearrange the equation

Rearranging gives us a standard quadratic equation:

$$ x^2 - 6x - 15 = 0 $$

5. Use the quadratic formula

To find the value of $x$, we can apply the quadratic formula, which is:

$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Here, $a = 1$, $b = -6$, and $c = -15$.

6. Calculate the discriminant

Calculate the discriminant:

$$ b^2 - 4ac = (-6)^2 - 4(1)(-15) = 36 + 60 = 96 $$

7. Substitute into the quadratic formula

Substituting $b$, $a$, and the discriminant into the quadratic formula gives:

$$ x = \frac{6 \pm \sqrt{96}}{2} $$

8. Simplify the square root and the expression

The square root of 96 simplifies:

$$ \sqrt{96} = \sqrt{16 \cdot 6} = 4\sqrt{6} $$

Substituting back, we get:

$$ x = \frac{6 \pm 4\sqrt{6}}{2} = 3 \pm 2\sqrt{6} $$

9. Determine the positive solution

Since $x$ must be positive, we take:

$$ x = 3 + 2\sqrt{6} $$

Now we can evaluate the numerical approximation of this expression.