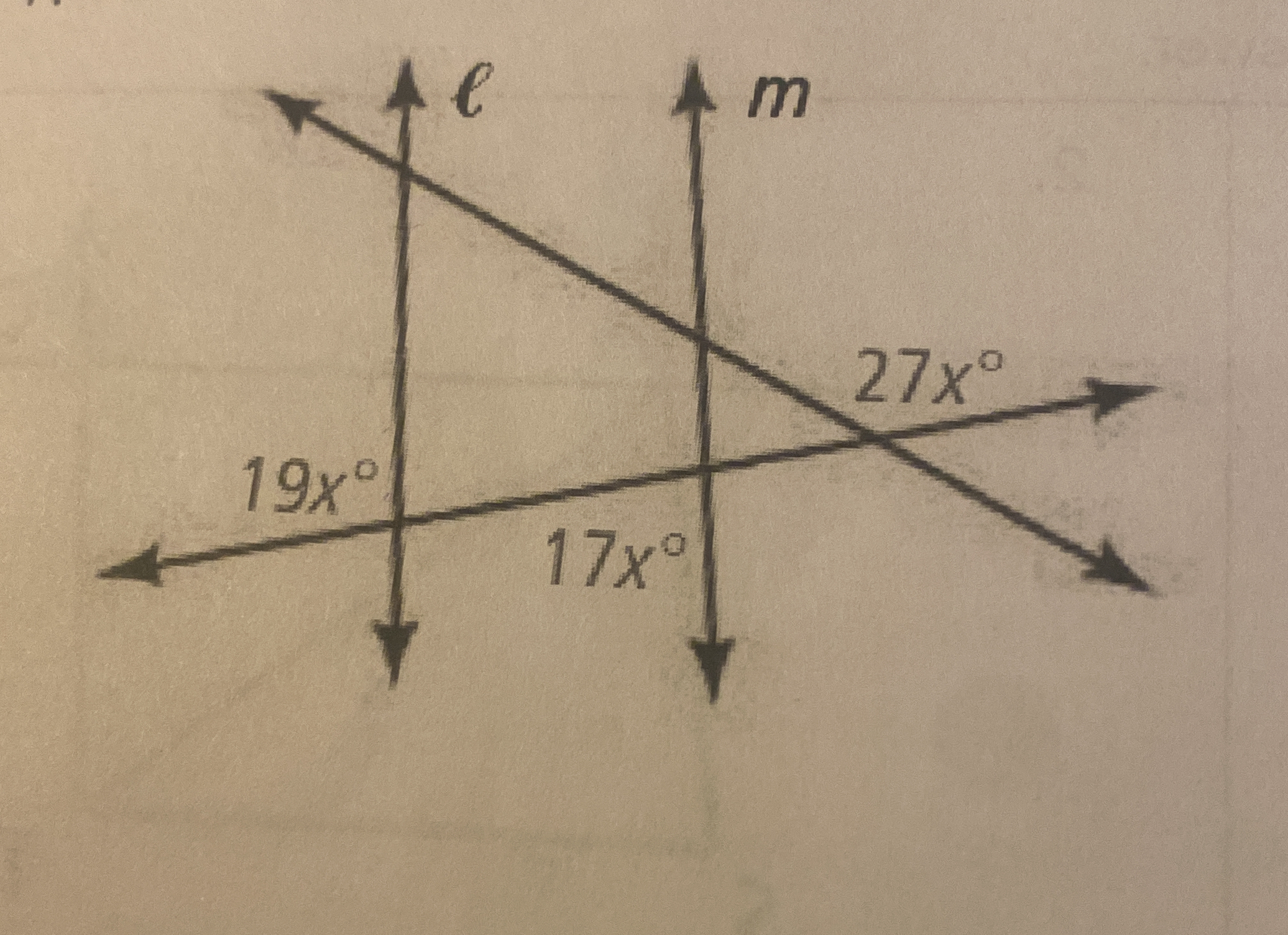
What is the value of x in the given diagram with angles 19x°, 17x°, and 27x°?
Understand the Problem
The question is asking to determine the value of x based on the angles formed when two lines intersect. It involves setting up an equation using the given angle expressions and solving for x.
Answer
The value of \( x \) is \( \frac{90}{23} \).
Answer for screen readers
The value of ( x ) is ( \frac{90}{23} ).
Steps to Solve
-
Identify angle relationships The angles formed at the intersection of two lines create pairs of supplementary angles. We can set up an equation using the angles given in the problem.
-
Set up the equation The angles $19x^\circ$ and $27x^\circ$ form a straight line, thus they are supplementary: $$ 19x + 27x = 180 $$
-
Combine like terms Combine the terms in the equation: $$ 46x = 180 $$
-
Solve for x To find the value of $x$, divide both sides by 46: $$ x = \frac{180}{46} $$
-
Simplify the fraction Simplifying the fraction, we can divide both the numerator and the denominator by 2: $$ x = \frac{90}{23} $$
The value of ( x ) is ( \frac{90}{23} ).
More Information
The angles formed at the intersection of two lines are important in geometry, especially regarding supplementary and vertical angles. Supplementary angles add up to ( 180^\circ ), which is a key concept in various geometric proofs.
Tips
- Not recognizing supplementary angles: A common mistake is forgetting that the angles must be added to equal ( 180^\circ ).
- Incorrectly simplifying fractions: Ensure that both the numerator and the denominator are simplified correctly to avoid mistakes in the final answer.
AI-generated content may contain errors. Please verify critical information