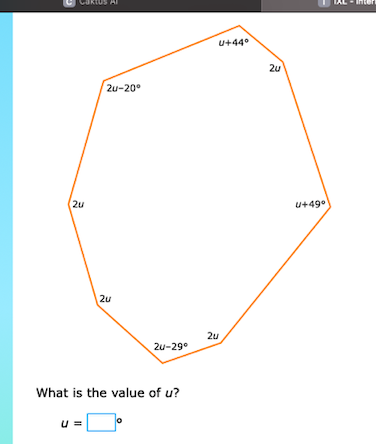
What is the value of u?
Understand the Problem
The question is asking for the value of the variable u in a polygon where the angles are expressed in terms of u. To solve this, we will need to use the properties of polygons and the sum of interior angles.
Answer
$u = 84.5^\circ$
Answer for screen readers
$u = 84.5^\circ$
Steps to Solve
- Find the number of sides of the polygon
The given polygon has 6 sides (hexagon).
- Calculate the sum of interior angles
The formula for the sum of interior angles of a polygon is given by: $$\text{Sum of interior angles} = (n - 2) \times 180^\circ$$ where $n$ is the number of sides. Since $n = 6$, we have: $$(6 - 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ$$
- Set up the equation for the angles
Now, we can express the sum of the angles in terms of $u$. The angles are:
- $u + 44^\circ$
- $2u - 20^\circ$
- $2u$ (twice)
- $u + 49^\circ$
- $2u - 29^\circ$
So we set up the equation: $$ (u + 44) + (2u - 20) + 2u + (u + 49) + (2u - 29) = 720 $$
- Combine like terms
Combine all the $u$ terms and the constant terms: $$ u + 2u + 2u + u + 2u + 44 - 20 + 49 - 29 = 720 $$ This simplifies to: $$ 8u + 44 - 20 + 49 - 29 = 720 $$
- Simplify the equation
Now simplify: $$ 8u + 44 - 20 + 49 - 29 = 720 $$ $$ 8u + 44 + 49 - 20 - 29 = 720 $$ $$ 8u + 44 + 49 - 20 - 29 = 720 $$ $$ 8u + 44 = 720 $$
- Isolate the variable
Now isolate $u$ by subtracting 44 from both sides: $$ 8u = 720 - 44 $$ $$ 8u = 676 $$
- Solve for $u$
Now, divide by 8: $$ u = \frac{676}{8} $$ $$ u = 84.5 $$
$u = 84.5^\circ$
More Information
The value of $u$ represents one of the angles in the hexagon and shows how different angle expressions can relate to the total angle sum in polygons.
Tips
- Forgetting to account for all angles when summing.
- Not applying the interior angle formula correctly for polygons with different numbers of sides.
AI-generated content may contain errors. Please verify critical information