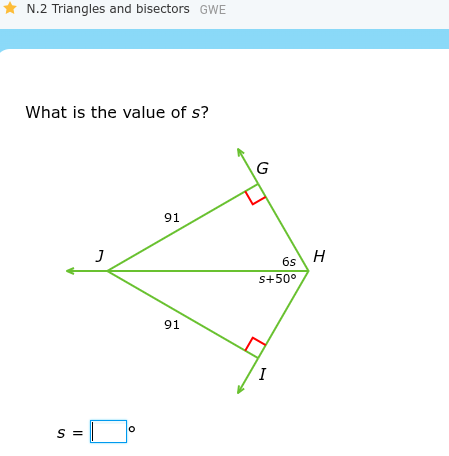
What is the value of s?
Understand the Problem
The question requires us to find the value of 's' given a geometric figure with certain angle and side measurements. We can use the properties of triangles and angle bisectors to solve for 's'. Essentially, we need to form equations based on the given information and solve for the unknown variable 's'.
Answer
$s = 10^{\circ}$
Answer for screen readers
$s = 10^{\circ}$
Steps to Solve
- Identify the two triangles
We observe two right-angled triangles: $\triangle GHJ$ and $\triangle IHJ$. We are given that $GJ = IJ = 91$. Also, $\angle G = \angle I = 90^\circ$.
- Congruence of the triangles
Since $GJ = IJ$ and $\angle G = \angle I = 90^\circ$, and $HJ$ is a common side, the two triangles $\triangle GHJ$ and $\triangle IHJ$ are congruent by the Hypotenuse-Leg (HL) congruence theorem.
- Equal angles at point $H$
Since the triangles are congruent, their corresponding angles are equal. Therefore, $\angle GHJ = \angle IHJ$. This gives us $6s = s + 50^\circ$.
- Solve for s
Subtract $s$ from both sides of the equation: $6s - s = s + 50^\circ - s$ $5s = 50^\circ$ Divide both sides by 5: $s = \frac{50^\circ}{5}$ $s = 10^\circ$
$s = 10^{\circ}$
More Information
The Hypotenuse-Leg (HL) congruence theorem is applicable only to right-angled triangles. It states that if the hypotenuse and one leg of a right-angled triangle are congruent to the hypotenuse and one leg of another right-angled triangle, then the two triangles are congruent.
Tips
A common mistake is to assume the triangles are similar without proving congruence. Also, algebraic errors while solving for $s$ can occur.
AI-generated content may contain errors. Please verify critical information