What is the value of $(\frac{2i}{1+i})^2$?
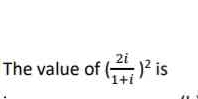
Understand the Problem
The question asks us to evaluate the expression $(\frac{2i}{1+i})^2$, which involves complex numbers. First simplify the fraction inside the parentheses, and then square the result to obtain the final answer.
Answer
$2i$
Answer for screen readers
$2i$
Steps to Solve
- Simplify the fraction $\frac{2i}{1+i}$
To simplify the fraction, we multiply the numerator and denominator by the conjugate of the denominator, which is $1-i$.
$\frac{2i}{1+i} = \frac{2i}{1+i} \cdot \frac{1-i}{1-i}$
- Multiply out the numerator and denominator
Multiplying out the numerator gives: $2i(1-i) = 2i - 2i^2 = 2i - 2(-1) = 2i + 2 = 2 + 2i$.
Multiplying out the denominator gives: $(1+i)(1-i) = 1 - i^2 = 1 - (-1) = 1 + 1 = 2$.
Therefore, $\frac{2i}{1+i} = \frac{2+2i}{2}$.
- Further simplification
We can divide both terms in the numerator by the denominator:
$\frac{2+2i}{2} = \frac{2}{2} + \frac{2i}{2} = 1 + i$.
- Square the result
Now we need to square the simplified fraction, which is $(1+i)^2$.
$(1+i)^2 = (1+i)(1+i) = 1 + i + i + i^2 = 1 + 2i + (-1) = 1 + 2i - 1 = 2i$.
$2i$
More Information
The imaginary unit $i$ is defined as $i = \sqrt{-1}$. Therefore, $i^2 = -1$.
Tips
A common mistake is not multiplying by the conjugate when simplifying complex fractions. Also, errors can be made when squaring the complex number. Be careful to properly distribute and remember that $i^2 = -1$.
AI-generated content may contain errors. Please verify critical information