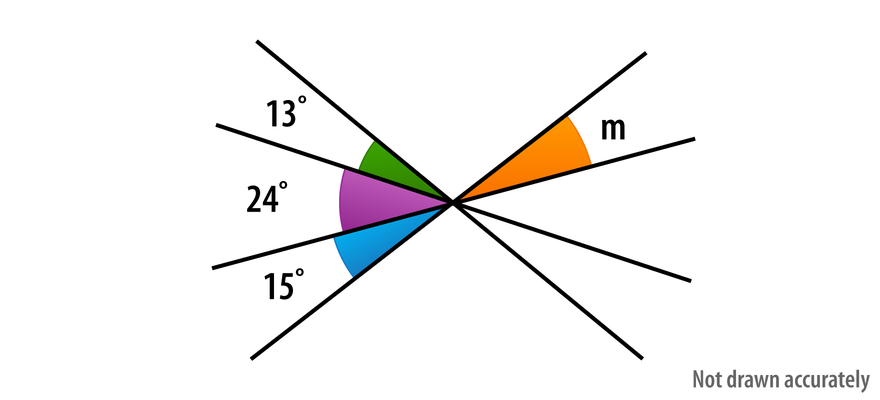
What is the value of angle m?
Understand the Problem
The question is asking for the measurement of angle m in the given diagram, where the sum of angles formed around a point must equal 360 degrees. We need to calculate m based on the other given angles (13°, 24°, and 15°).
Answer
The measurement of angle $m$ is \( 308^\circ \).
Answer for screen readers
The measurement of angle $m$ is ( 308^\circ ).
Steps to Solve
-
Identify Known Angles The angles given in the problem are $13^\circ$, $24^\circ$, and $15^\circ$.
-
Sum of Angles Around a Point The sum of all angles around a point is $360^\circ$. Therefore, we can set up the following equation: $$ 13^\circ + 24^\circ + 15^\circ + m = 360^\circ $$
-
Combine Known Angles Add the known angles together: $$ 13^\circ + 24^\circ + 15^\circ = 52^\circ $$
-
Set Up the Final Equation Now substitute the sum into the equation: $$ 52^\circ + m = 360^\circ $$
-
Isolate Angle m To find $m$, subtract $52^\circ$ from both sides: $$ m = 360^\circ - 52^\circ $$
-
Calculate the Value of m Now do the calculation: $$ m = 308^\circ $$
The measurement of angle $m$ is ( 308^\circ ).
More Information
This problem illustrates the concept of angles in a circle and the fact that the total measurement of angles around a point is always $360^\circ$. This principle is fundamental in geometry and can be applied in various real-world contexts, like navigation and architecture.
Tips
- A common mistake is forgetting to include all known angles before calculating $m$. Always ensure to sum all provided angles to avoid errors.
- Another mistake is miscalculating the subtraction; double-check arithmetic is important to arrive at the correct angle.
AI-generated content may contain errors. Please verify critical information