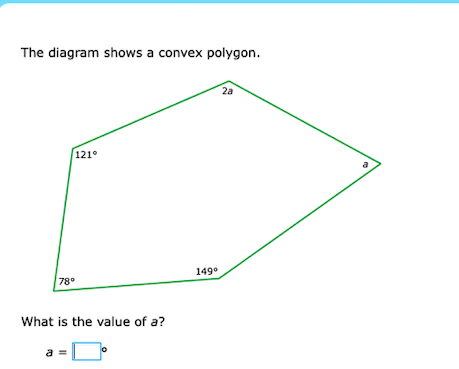
What is the value of a?
Understand the Problem
The question is asking for the value of the angle 'a' in a convex polygon, given the measures of the other angles and the relationship between angle 'a' and the angle labeled '2a'. To find 'a', we will need to use the properties of polygons, particularly that the sum of the interior angles of a polygon can be calculated.
Answer
The value of \( a \) is \( 64^\circ \).
Answer for screen readers
The value of ( a ) is ( 64^\circ ).
Steps to Solve
- Calculate the sum of interior angles of the polygon
For a polygon with ( n ) sides, the sum of the interior angles can be calculated using the formula:
$$ \text{Sum of interior angles} = (n - 2) \times 180^\circ $$
In this case, we know there are 5 angles (the polygon looks like a pentagon), so:
$$ \text{Sum} = (5 - 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ $$
- Set up the equation for the angles
The angles in the polygon are given as ( a ), ( 2a ), ( 121^\circ ), ( 78^\circ ), and ( 149^\circ ). We can set up the equation:
$$ a + 2a + 121^\circ + 78^\circ + 149^\circ = 540^\circ $$
- Combine like terms
Combine the ( a ) terms and the constant angles:
$$ 3a + 121^\circ + 78^\circ + 149^\circ = 540^\circ $$
- Simplify the equation
Add the constant angles together:
$$ 3a + 348^\circ = 540^\circ $$
- Isolate ( a )
Subtract ( 348^\circ ) from both sides:
$$ 3a = 540^\circ - 348^\circ $$
This simplifies to:
$$ 3a = 192^\circ $$
- Solve for ( a )
Divide both sides by 3:
$$ a = \frac{192^\circ}{3} = 64^\circ $$
The value of ( a ) is ( 64^\circ ).
More Information
In a convex polygon, the sum of the interior angles is a crucial property. In a pentagon, it equals 540 degrees, which is essential for solving for unknown angles.
Tips
- Forgetting to account for the number of sides when calculating the sum of interior angles.
- Misidentifying the polygon type (e.g., thinking it’s a different polygon with a different angle sum).
AI-generated content may contain errors. Please verify critical information