What is the slope of the other diagonal?

Steps to Solve

1. Identify the coordinates of points V and T

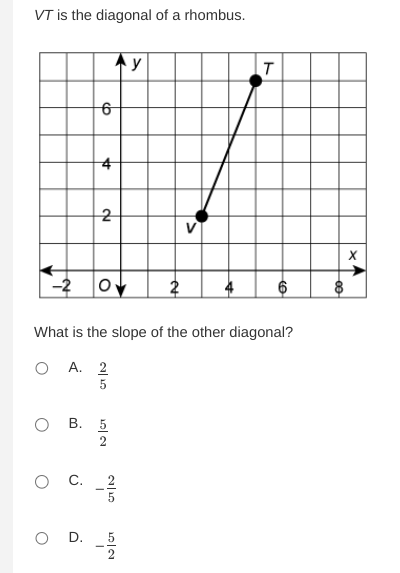
From the graph, we can read the coordinates of points V and T:

• Point ( V ) is at ( (2, 2) )
• Point ( T ) is at ( (4, 6) )

2. Calculate the slope of diagonal VT

The formula for the slope ( m ) between two points ( (x_1, y_1) ) and ( (x_2, y_2) ) is given by:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

For points ( V ) and ( T ):

• ( (x_1, y_1) = (2, 2) )
• ( (x_2, y_2) = (4, 6) )

Now plug in the values:

$$ m_{VT} = \frac{6 - 2}{4 - 2} = \frac{4}{2} = 2 $$

3. Use the properties of the rhombus

In a rhombus, the diagonals bisect each other at right angles. If the slope of one diagonal is ( m_{1} ), the slope of the other diagonal ( m_{2} ) can be found using the formula:

$$ m_{1} \cdot m_{2} = -1 $$

From step 2, we know ( m_{VT} = 2 ). Now we can set up the equation:

$$ 2 \cdot m_{2} = -1 $$

4. Solve for the slope of the other diagonal

Rearranging the equation gives:

$$ m_{2} = \frac{-1}{2} $$

This is the slope of the other diagonal.