What is the slope of the line 4x - 8y + 3 = 0?
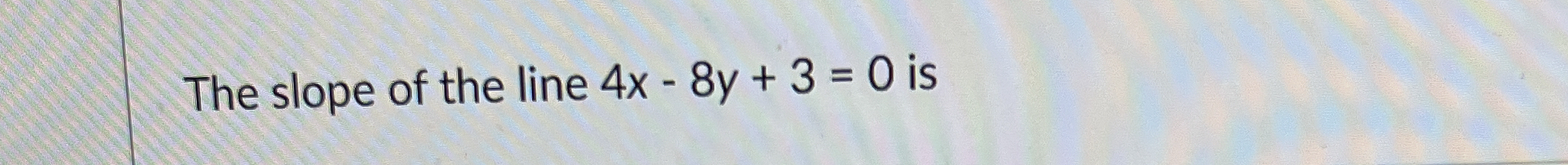
Understand the Problem
The question asks to find the slope of the line given by the equation 4x - 8y + 3 = 0. To solve this, we should rearrange the equation into slope-intercept form (y = mx + b), where 'm' represents the slope.
Answer
$\frac{1}{2}$
Answer for screen readers
The slope of the line is $\frac{1}{2}$.
Steps to Solve
-
Isolate the 'y' term Start with the given equation: $4x - 8y + 3 = 0$. We want to isolate the term containing $y$. Subtract $4x$ and $3$ from both sides of the equation: $$-8y = -4x - 3$$
-
Solve for 'y' Divide both sides of the equation by $-8$ to solve for $y$: $$y = \frac{-4x - 3}{-8}$$
-
Simplify the equation Simplify the fraction by dividing each term in the numerator by $-8$: $$y = \frac{-4x}{-8} + \frac{-3}{-8}$$ $$y = \frac{1}{2}x + \frac{3}{8}$$
-
Identify the slope The equation is now in slope-intercept form, $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept. In this case, $m = \frac{1}{2}$.
The slope of the line is $\frac{1}{2}$.
More Information
The slope-intercept form of a linear equation ($y = mx + b$) makes it easy to identify the slope ($m$) and y-intercept ($b$) of the line. The slope represents the rate of change of $y$ with respect to $x$, and the y-intercept is the point where the line crosses the y-axis.
Tips
A common mistake is to incorrectly perform the arithmetic when isolating $y$. For example, forgetting to divide every term by $-8$, or making sign errors. Another common mistake is stopping after isolating $-8y$ and not dividing to solve for just $y$.
AI-generated content may contain errors. Please verify critical information