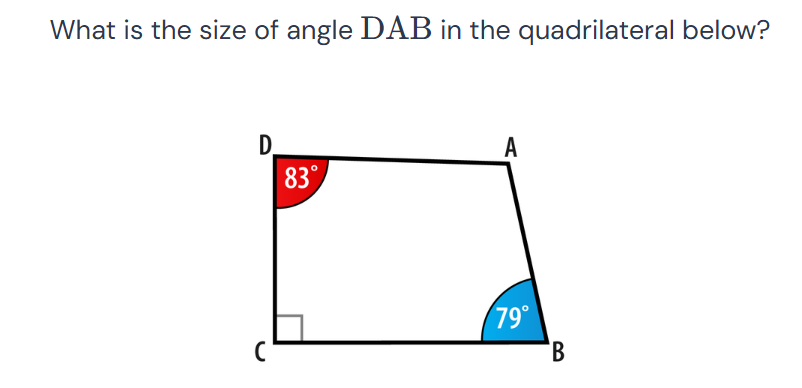
What is the size of angle DAB in the quadrilateral below?
Understand the Problem
The question asks for the measure of angle DAB in the given quadrilateral. We need to use the properties of quadrilaterals (sum of angles) to find the missing angle.
Answer
$108^{\circ}$
Answer for screen readers
The size of angle DAB is $108^{\circ}$.
Steps to Solve
- Identify the known angles
From the image, we know the following angles:
- Angle D = $83^{\circ}$
- Angle B = $79^{\circ}$
- Angle C = $90^{\circ}$ (indicated by the square symbol)
- Recall the sum of angles in a quadrilateral
The sum of interior angles in any quadrilateral is $360^{\circ}$.
- Set up an equation to find angle A (DAB)
Let angle A be represented as $x$. We can write the equation: $$x + 83^{\circ} + 79^{\circ} + 90^{\circ} = 360^{\circ}$$
- Solve for x
Combine the known angles: $$x + 252^{\circ} = 360^{\circ}$$ Subtract $252^{\circ}$ from both sides: $$x = 360^{\circ} - 252^{\circ}$$ $$x = 108^{\circ}$$
The size of angle DAB is $108^{\circ}$.
More Information
A quadrilateral is a polygon with four sides, four vertices and four angles.
Tips
A common mistake is forgetting that the right angle is $90^{\circ}$ or using the wrong total sum of angles for a quadrilateral (which is $360^{\circ}$).
AI-generated content may contain errors. Please verify critical information