What is the rate of change of y with respect to x?
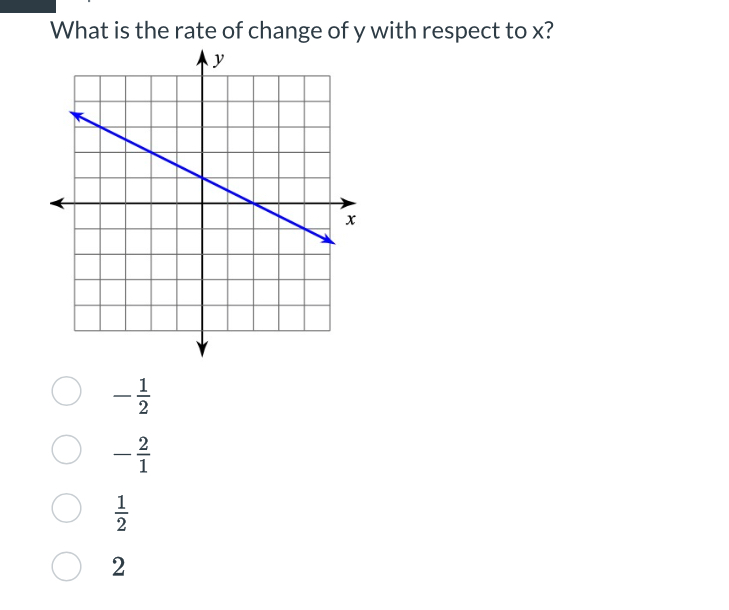
Understand the Problem
The question is asking for the rate of change of the variable y in relation to x, which is typically determined by analyzing the slope of a given line on a Cartesian coordinate system. It requires calculating the slope from the graph provided.
Answer
The rate of change is $-1$.
Answer for screen readers
The rate of change of $y$ with respect to $x$ is $-1$.
Steps to Solve
-
Identify Two Points on the Line Select two clear points on the blue line from the graph. For example, let’s choose the points $(0, 1)$ and $(2, -1)$.
-
Determine the Change in y (Δy) Calculate the difference in the y-coordinates of the two points. $$ \Delta y = y_2 - y_1 = -1 - 1 = -2 $$
-
Determine the Change in x (Δx) Calculate the difference in the x-coordinates of the two points. $$ \Delta x = x_2 - x_1 = 2 - 0 = 2 $$
-
Calculate the Slope (Rate of Change) Using the slope formula $\frac{\Delta y}{\Delta x}$, substitute the values found above. $$ \text{slope} = \frac{\Delta y}{\Delta x} = \frac{-2}{2} = -1 $$
The rate of change of $y$ with respect to $x$ is $-1$.
More Information
The rate of change (slope) represents how much $y$ changes for a one-unit change in $x$. In this case, for every unit increase in $x$, $y$ decreases by 1.
Tips
- Choosing Incorrect Points: Make sure to select points that clearly lie on the line.
- Calculating the Change in y Wrongly: Remember to subtract the values correctly (final - initial).
