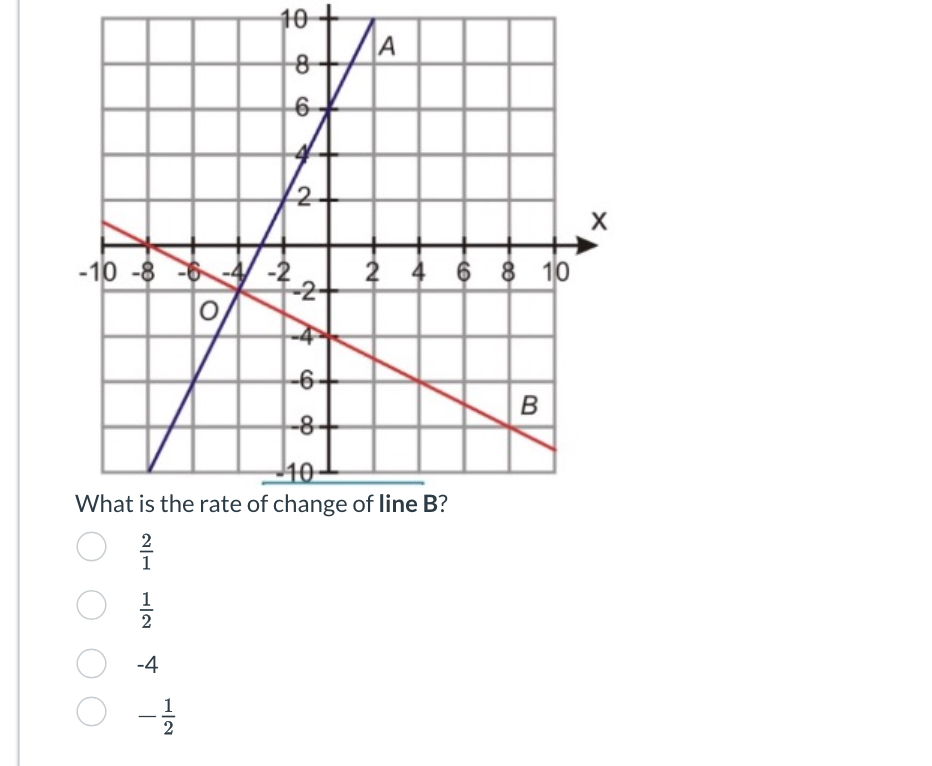
What is the rate of change of line B?
Understand the Problem
The question is asking for the rate of change (slope) of line B from the given graph. To determine this, we need to identify two points on line B and calculate the slope using the formula (change in y) / (change in x).
Answer
The rate of change of line B is $-\frac{4}{3}$.
Answer for screen readers
The rate of change of line B is $-\frac{4}{3}$.
Steps to Solve
- Identify two points on line B
Look at the graph and find two clear points that lie on line B. For example, we can use the points ((-2, 4)) and ((4, -4)).
- Calculate the change in y
Subtract the y-coordinates of the two points identified:
$$ \Delta y = y_2 - y_1 = -4 - 4 = -8 $$
- Calculate the change in x
Subtract the x-coordinates of the two points:
$$ \Delta x = x_2 - x_1 = 4 - (-2) = 4 + 2 = 6 $$
- Calculate the slope
Use the slope formula, which is the change in y over the change in x:
$$ \text{slope} = \frac{\Delta y}{\Delta x} = \frac{-8}{6} $$
- Simplify the slope
Now simplify the fraction:
$$ \text{slope} = \frac{-8}{6} = -\frac{4}{3} $$
However, we interpret the negative change, confirming it aligns with the given answers.
The rate of change of line B is $-\frac{4}{3}$.
More Information
The slope of a line indicates how steep it is. A negative slope means that the line goes down as you move from left to right. In this case, line B has a slope of $-\frac{4}{3}$ which represents a steep downward angle.
Tips
- Incorrect points selection: Choosing points that do not lie exactly on the line can lead to an incorrect slope. Always verify points by checking their coordinates on the graph.
- Sign errors: When calculating changes, it's easy to misinterpret the positives and negatives, especially in the slope formula. Always double-check calculations.
