What is the rate of change of line A?
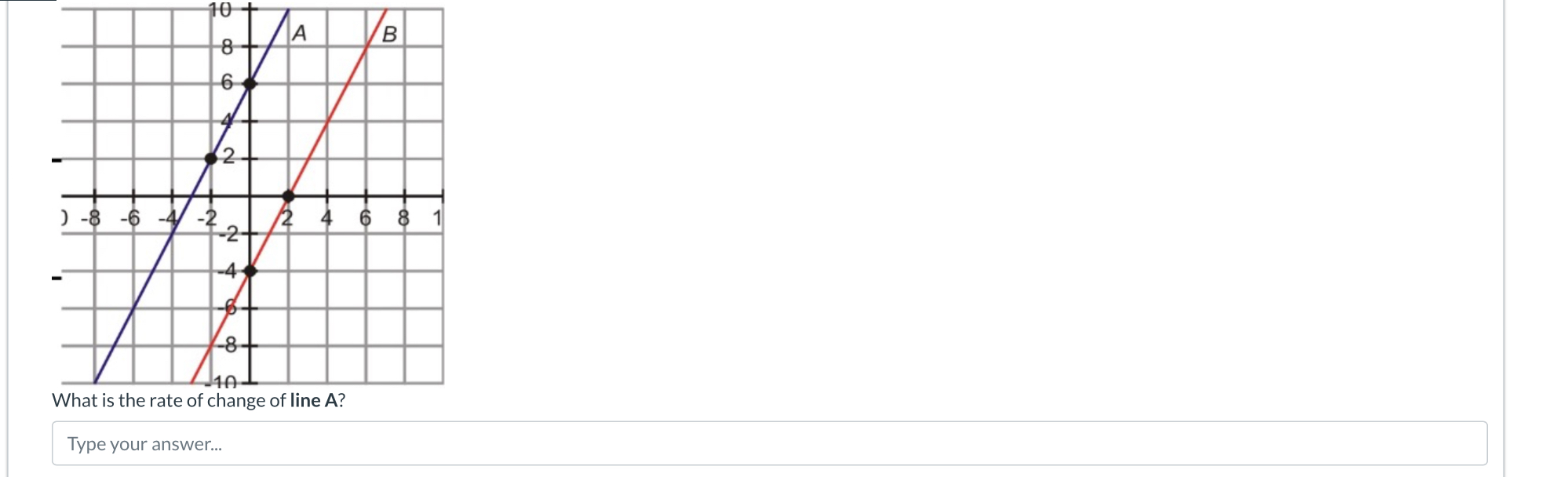
Understand the Problem
The question is asking for the rate of change of line A on a graph, which requires understanding the slope of the line defined by two points on it.
Answer
The rate of change of line A is $-3$.
Answer for screen readers
The rate of change of line A is $-3$.
Steps to Solve
- Identify two points on line A
From the graph, we see that line A intersects the y-axis at (0, 6) and passes through another point at (2, 0).
- Use the slope formula
The slope (rate of change) of a line can be calculated using the formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Where:
- $(x_1, y_1)$ is the first point (0, 6)
- $(x_2, y_2)$ is the second point (2, 0)
- Substitute the points into the formula
Plugging in the values:
$$ m = \frac{0 - 6}{2 - 0} = \frac{-6}{2} $$
- Simplify to find the slope
Now simplify the fraction:
$$ m = -3 $$
This means the slope of line A is -3, which indicates that for every 1 unit increase in x, y decreases by 3 units.
The rate of change of line A is $-3$.
More Information
The slope of a line describes how steep it is and the direction of the line. A negative slope, like in this case, indicates that the line is declining as it moves from left to right on the graph.
Tips
- Forgetting to switch the order of coordinates when calculating change in y and change in x.
- Misinterpreting the slope as positive when it should be negative.
