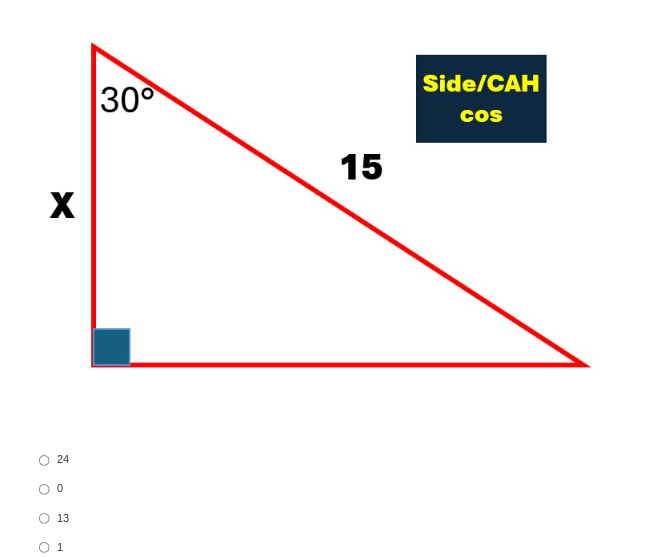
What is the length of side X in a right triangle with an angle of 30 degrees and an adjacent side of 15?

Steps to Solve

1. Identify the triangle sides using trigonometry

In a right triangle, the cosine function relates the adjacent side to the hypotenuse. The formula is given by:

$$ \cos(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}} $$

Here, the angle $\theta$ is $30^\circ$, the adjacent side is $15$, and we are trying to find the hypotenuse ($X$).

2. Set up the equation using the cosine function

Using the cosine function:

$$ \cos(30^\circ) = \frac{15}{X} $$

3. Solve for the hypotenuse $X$

Rearranging the equation to solve for $X$ gives:

$$ X = \frac{15}{\cos(30^\circ)} $$

4. Calculate $\cos(30^\circ)$

The value of $\cos(30^\circ)$ is known to be:

$$ \cos(30^\circ) = \frac{\sqrt{3}}{2} $$

5. Substitute and calculate $X$

Now substituting the value of $\cos(30^\circ)$:

$$ X = \frac{15}{\frac{\sqrt{3}}{2}} $$

Multiplying by the reciprocal:

$$ X = 15 \cdot \frac{2}{\sqrt{3}} $$

6. Simplify the expression for $X$

Calculating this gives:

$$ X = \frac{30}{\sqrt{3}} $$

Rationalize the denominator:

$$ X = \frac{30 \cdot \sqrt{3}}{3} $$

Final calculation yields:

$$ X = 10\sqrt{3} $$

7. Approximate the numerical value

Approximating $\sqrt{3} \approx 1.732$ gives:

$$ X \approx 10 \times 1.732 \approx 17.32 $$