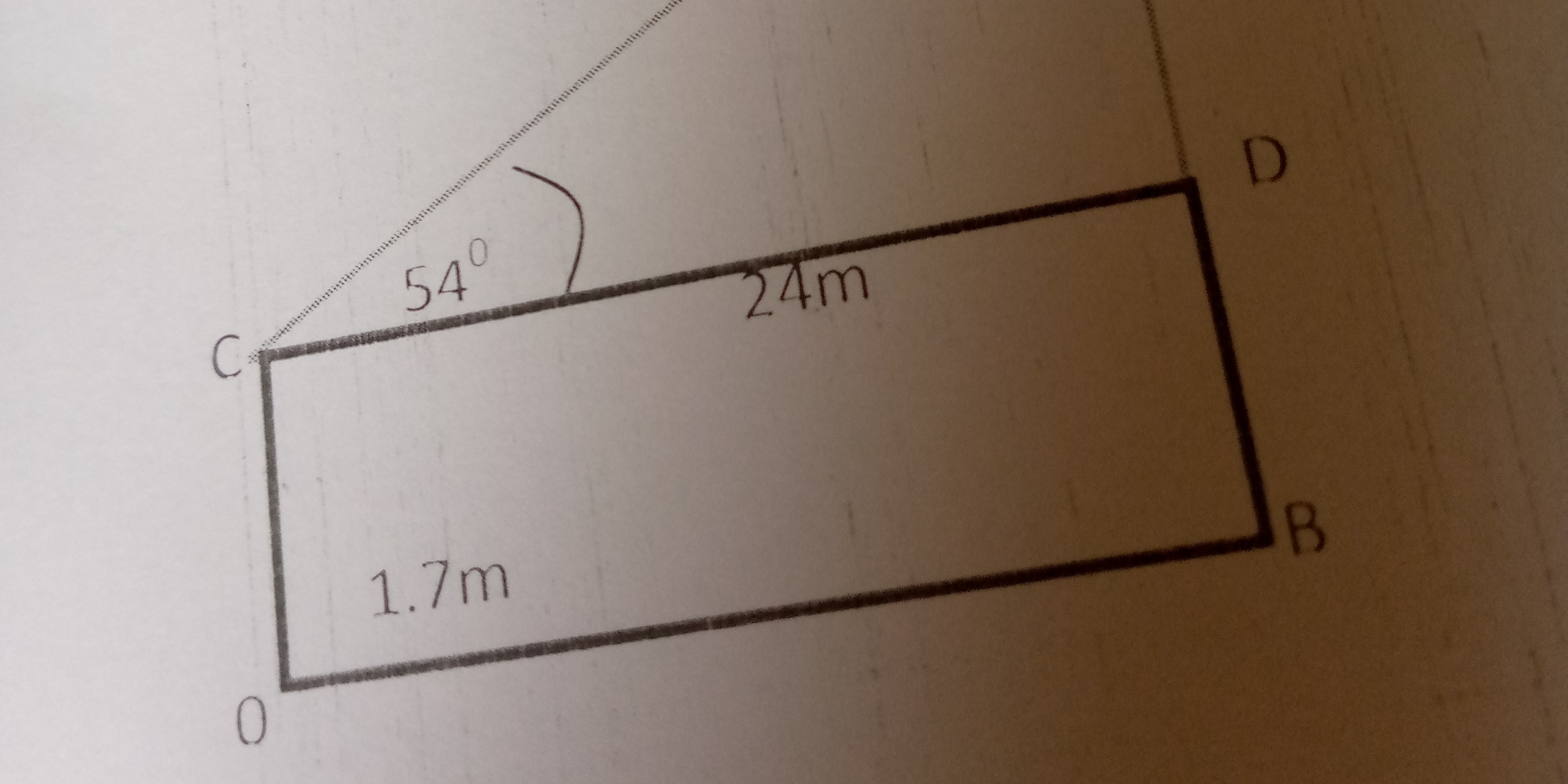
What is the length of line CB in the provided diagram?

Steps to Solve

1. Identify the unknown length

We need to find the length of the line extending from point $C$ at a $54^\circ$ angle to the side $OD$. Let's label the point where the line intersects $OD$ as $E$. Thus, we need to find the length of $CE$.

2. Analyze the geometry of the problem

We can see that we have a rectangle $CODB$. We know that $CD = 24m$ and $CO = 1.7m$. We also have an angle of $54^\circ$ at point $C$. We can use the tangent function to relate the sides of the right triangle $\triangle COE$.

3. Calculate the length of $OE$

Let $OE = x$. We have $\angle E CO = 54^\circ$. So, $\tan(54^\circ) = \frac{OE}{CO} = \frac{x}{1.7}$ $x = 1.7 \times \tan(54^\circ)$.

4. Find $\tan(54^\circ)$

$\tan(54^\circ) \approx 1.376$

5. Calculate $OE$

$OE = 1.7 \times 1.376 \approx 2.3392$

6. Calculate $DE$

Since $OD = CD = 24m$, then $DE = OD - OE = 24 - 2.3392 = 21.6608$.

7. Calculate $CE$ We can use the Pythagorean theorem to find the length of $CE$. In $\triangle COE$: $CE^2 = CO^2 + OE^2$ $CE^2 = 1.7^2 + 2.3392^2$ $CE^2 = 2.89 + 5.4718$ $CE^2 = 8.3618$ $CE = \sqrt{8.3618} \approx 2.89m $