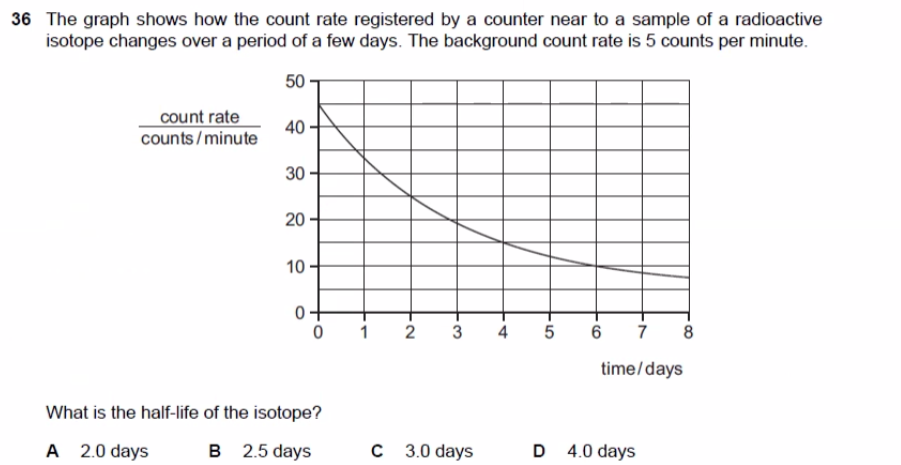
What is the half-life of the isotope?
Understand the Problem
The question asks us to determine the half-life of a radioactive isotope based on a graph showing the count rate over time. We need to account for the background count rate to find the time it takes for the count rate to reduce by half.
Answer
A. 2.0 days
The half-life of the isotope is 2.0 days, so the answer is A.
Answer for screen readers
The half-life of the isotope is 2.0 days, so the answer is A.
More Information
The half-life is the time it takes for half of the radioactive isotope to decay. The initial count rate is 45 counts per minute (50 total - 5 background). Half of 45 is 22.5. 22.5 + 5 background = 27.5 counts per minute. Looking at the graph, 27.5 counts per minute occurs at 2 days.
Tips
Remember to subtract the background radiation from the total count rate before determining the half-life from the graph. Failing to account for background radiation is a common mistake.
Sources
- Half-life | Definition & Facts - Britannica - britannica.com
- 11.2: Half-Life - Chemistry LibreTexts - chem.libretexts.org
- RadTown Radioactive Atom Activity 5: Half-Life | US EPA - epa.gov
AI-generated content may contain errors. Please verify critical information