What is the equation of the line?
Understand the Problem
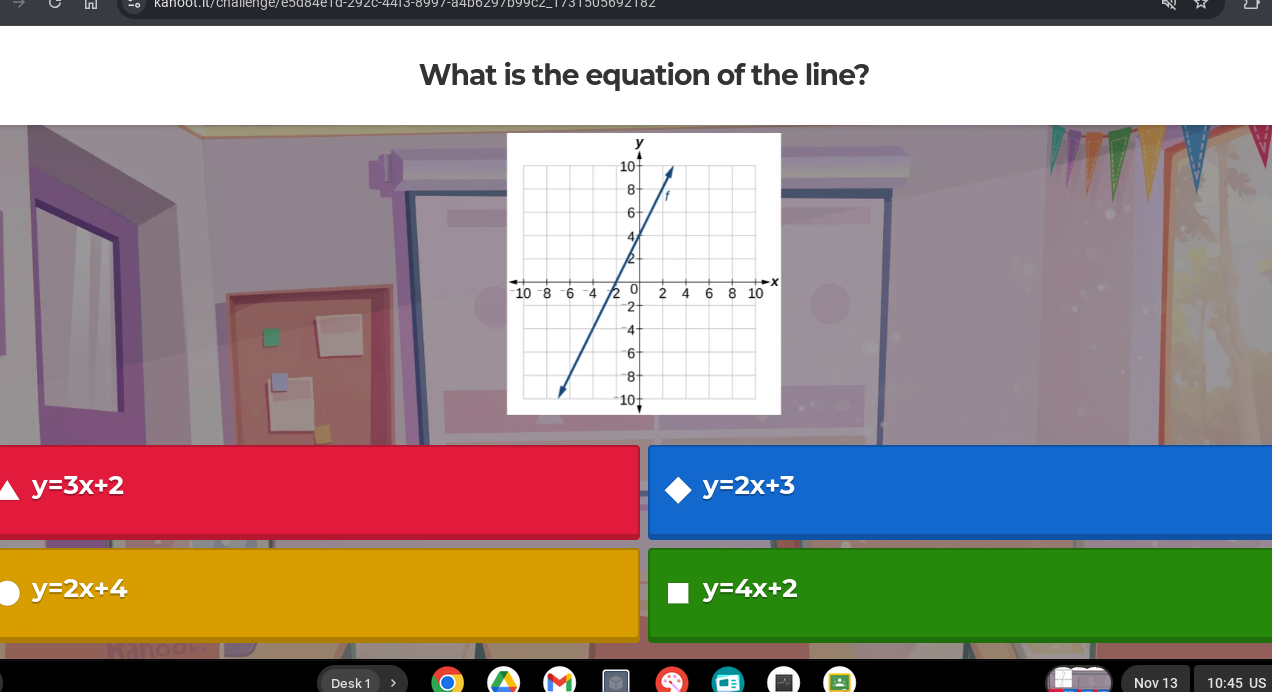
The question is asking for the equation of a line given a graph. We need to analyze the graph to determine the correct linear equation from the provided choices.
Answer
The equation of the line is \( y = 3x + 2 \).
Answer for screen readers
The equation of the line is ( y = 3x + 2 ).
Steps to Solve
- Identify the slope of the line To find the equation of the line, we need to determine its slope (m). This can be done by identifying two points on the line. For example, let's assume we see points at ( (0, 2) ) and ( (2, 8) ).
The slope ( m ) can be calculated using the formula: $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$ Substituting in the values: $$ m = \frac{8 - 2}{2 - 0} = \frac{6}{2} = 3 $$
-
Identify the y-intercept The y-intercept is the value of ( y ) when ( x = 0 ). From our points, we can see that when ( x = 0 ), ( y = 2 ). Thus, the y-intercept ( b ) is 2.
-
Write the equation of the line Using the slope-intercept form of the equation of a line, which is: $$ y = mx + b $$ we substitute ( m ) and ( b ): $$ y = 3x + 2 $$
-
Compare the equation with the options Now we compare our derived equation ( y = 3x + 2 ) with the options given in the question to identify the correct choice.
The equation of the line is ( y = 3x + 2 ).
More Information
The equation of a line in slope-intercept form ( y = mx + b ) consists of the slope ( m ) and the y-intercept ( b ). In this case, the slope indicates how steeply the line rises, and the y-intercept shows where the line crosses the y-axis.
Tips
- Assuming the slope is always positive: The slope can be negative; make sure to consider the direction of the line when selecting points.
- Forgetting to simplify fractions: Ensure to simplify the slope expression correctly to avoid calculation errors.
- Not checking the options: Always compare the derived equation with all provided options to ensure a correct match.
AI-generated content may contain errors. Please verify critical information