What is the domain of the function y = √(2x² - 5x - 12)?
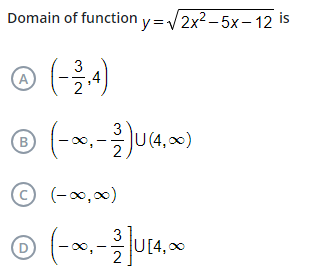
Understand the Problem
The question is asking for the domain of the function y = √(2x² - 5x - 12), specifically the set of values for x that will yield real outputs for y. This will involve finding when the expression under the square root is non-negative.
Answer
The domain of the function is $(-\infty, -\frac{3}{2}] \cup [4, \infty)$.
Answer for screen readers
The domain of the function ( y = \sqrt{2x^2 - 5x - 12} ) is $(-\infty, -\frac{3}{2}] \cup [4, \infty)$.
Steps to Solve
- Set the expression under the square root greater than or equal to zero
To find the domain of the function ( y = \sqrt{2x^2 - 5x - 12} ), we need to solve the inequality:
$$ 2x^2 - 5x - 12 \geq 0 $$
- Factor the quadratic expression
Next, we will factor the quadratic expression. We need to find two numbers that multiply to ( 2 \times -12 = -24 ) and add to ( -5 ). The factors are ( -8 ) and ( 3 ). We can rewrite the expression as:
$$ 2x^2 - 8x + 3x - 12 = 0 $$
Now, we can factor by grouping:
$$ 2x(x - 4) + 3(x - 4) = 0 $$
Thus, we have:
$$ (2x + 3)(x - 4) = 0 $$
- Find the critical points
Setting each factor to zero gives us the critical points:
$$ 2x + 3 = 0 \implies x = -\frac{3}{2} $$
$$ x - 4 = 0 \implies x = 4 $$
- Sign analysis
Now, we will test intervals defined by these critical points ( (-\infty, -\frac{3}{2}) ), ( (-\frac{3}{2}, 4) ), and ( (4, \infty) ) to determine where the expression is non-negative.
- For ( x < -\frac{3}{2} ), choose ( x = -2 ):
$$ 2(-2)^2 - 5(-2) - 12 = 8 + 10 - 12 = 6 ; (> 0) $$
- For ( -\frac{3}{2} < x < 4 ), choose ( x = 0 ):
$$ 2(0)^2 - 5(0) - 12 = -12 ; (< 0) $$
- For ( x > 4 ), choose ( x = 5 ):
$$ 2(5)^2 - 5(5) - 12 = 50 - 25 - 12 = 13 ; (> 0) $$
- Write the solution in interval notation
The quadratic expression ( 2x^2 - 5x - 12 ) is non-negative in the intervals ( (-\infty, -\frac{3}{2}] ) and ( [4, \infty) ). Therefore, the domain of the function is:
$$ (-\infty, -\frac{3}{2}] \cup [4, \infty) $$
The domain of the function ( y = \sqrt{2x^2 - 5x - 12} ) is $(-\infty, -\frac{3}{2}] \cup [4, \infty)$.
More Information
The domain is critical for understanding where the function is defined. In this case, the function outputs real numbers only when the expression under the square root is non-negative.
Tips
- Failing to test intervals properly for the sign of the quadratic expression.
- Ignoring the endpoints while determining the intervals which can lead to incorrect interval notation.
AI-generated content may contain errors. Please verify critical information