What is the distance covered by the object at the time between 0s to 10s?

Understand the Problem

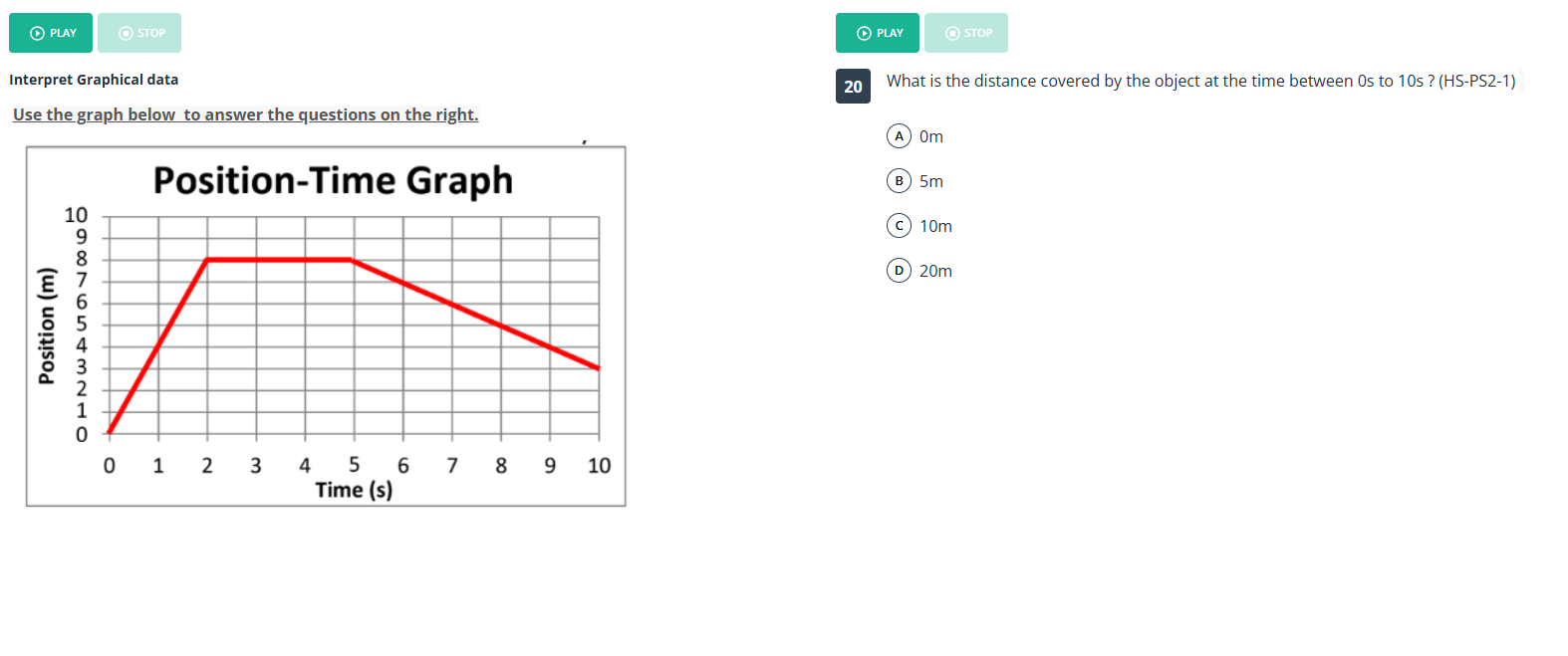
The question is asking to determine the distance covered by an object based on a position-time graph over a specific time interval from 0 to 10 seconds. We will analyze the graph's data to find the total displacement over this period.

Answer

The distance covered by the object is $16$ m.

Steps to Solve

Identify Key Points on the Graph Look at the position-time graph. At $t = 0$ seconds, the position is $0$ m. At $t = 2$ seconds, the position reaches $8$ m. The object remains at $8$ m from $t = 2$ to $t = 7$ seconds. Finally, the object moves down to $0$ m at $t = 10$ seconds.
Calculate Displacements Determine the total distance covered during each segment of motion:
- From $0$ to $2$ seconds: Distance = $8 - 0 = 8$ m
- From $2$ to $7$ seconds: Distance = $0$ m (stays at $8$ m)
- From $7$ to $10$ seconds: Distance = $8 - 0 = 8$ m
Add Distances for Total Distance Total distance covered is the sum of all segments: $$ \text{Total Distance} = 8 , \text{m} + 0 , \text{m} + 8 , \text{m} = 16 , \text{m}$$
Consider Options in the Question Review the available answer choices:
- A) 0 m
- B) 5 m
- C) 10 m
- D) 20 m
  Since 16 m is not among the options listed, verify the calculations.

The total distance covered by the object from $0$ to $10$ seconds is $16$ m.

More Information

The distance covered by an object in motion can often differ from displacement, as displacement considers direction. This problem illustrates how to analyze a position-time graph and compute total distance traveled.

Tips

Ignoring periods of rest: During the time the object doesn't move (between $2$ and $7$ seconds), some might mistakenly calculate this as movement. Always account for stationary periods.
Confusing displacement with distance: Displacement only considers the initial and final positions but does not add up all segments. Make sure to differentiate between the two.

Thank you for voting!