What is the derivative of x_2 = (1/2)(-x_1^2 + u)?
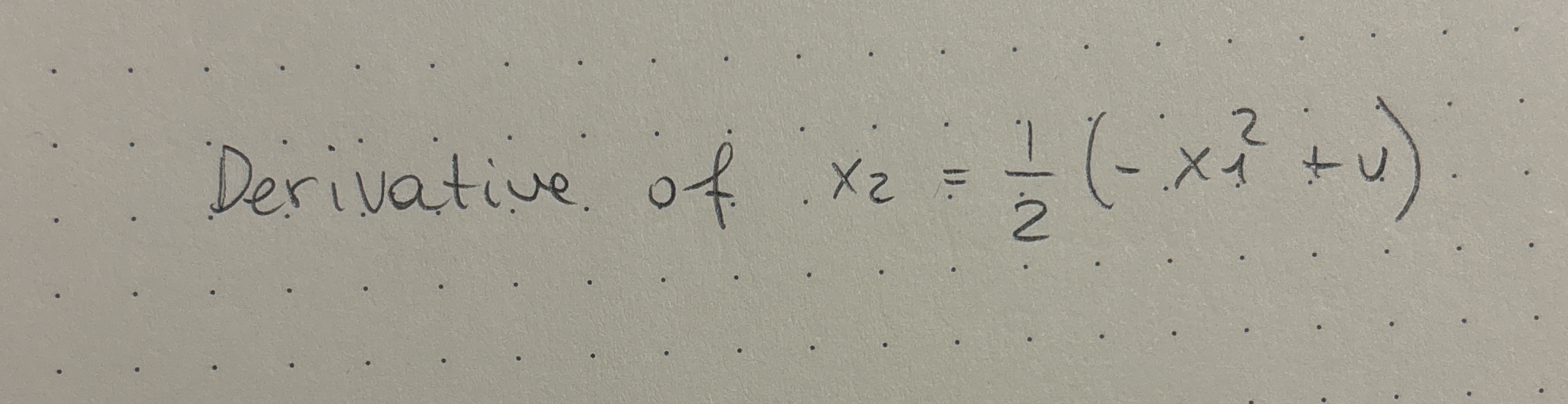
Understand the Problem
The question asks to compute the derivative of (x_2) with respect to (x_1), where (x_2 = \frac{1}{2}(-x_1^2 + u)) and (u) is presumably a constant. To solve this, we'll apply the power rule and constant multiple rule of differentiation.
Answer
$$-x_1$$
Answer for screen readers
$$ \frac{dx_2}{dx_1} = -x_1 $$
Steps to Solve
-
Rewrite the equation First, rewrite the equation to distribute the $\frac{1}{2}$: $$ x_2 = \frac{1}{2}(-x_1^2 + u) = -\frac{1}{2}x_1^2 + \frac{1}{2}u $$
-
Apply the power rule Apply the power rule to the first term. The power rule states that $\frac{d}{dx}(x^n) = nx^{n-1}$. Therefore, the derivative of $-\frac{1}{2}x_1^2$ with respect to $x_1$ is: $$ \frac{d}{dx_1}(-\frac{1}{2}x_1^2) = -\frac{1}{2}(2x_1^{2-1}) = -x_1 $$
-
Derivative of a constant Since $u$ is a constant (with respect to $x_1$), then $\frac{1}{2}u$ is also a constant. The derivative of a constant is zero: $$ \frac{d}{dx_1}(\frac{1}{2}u) = 0 $$
-
Combine the results Add the derivatives of each term to find the derivative of the entire expression: $$ \frac{dx_2}{dx_1} = -x_1 + 0 = -x_1 $$
$$ \frac{dx_2}{dx_1} = -x_1 $$
More Information
The derivative of $x_2$ with respect to $x_1$ is $-x_1$. This represents the instantaneous rate of change of $x_2$ as $x_1$ changes.
Tips
A common mistake is forgetting to apply the power rule correctly, especially when there's a constant multiple involved and another mistake is not realizing that the derivative of a constant is zero
AI-generated content may contain errors. Please verify critical information