What is the cost of 1 cup of coffee?
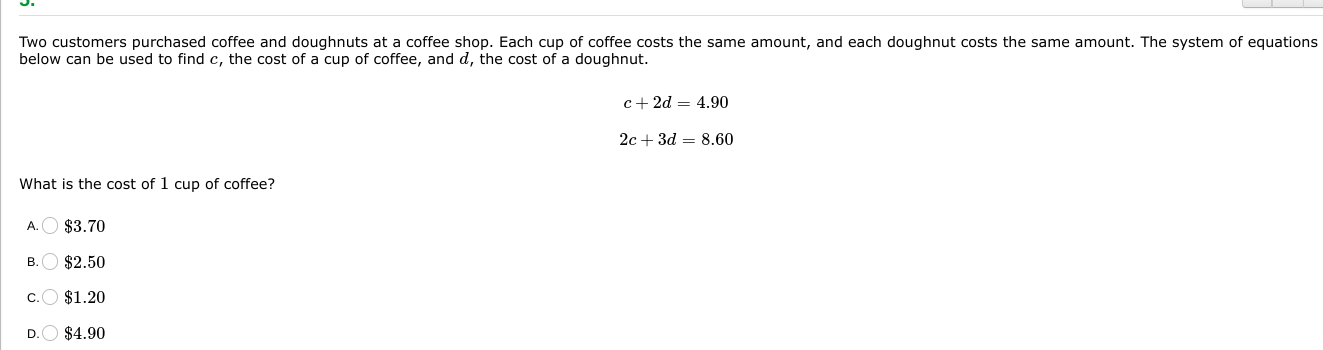
Understand the Problem
The question is asking to solve a system of equations to determine the cost of one cup of coffee. The equations provided relate the costs of coffee and doughnuts purchased by two customers.
Answer
The cost of 1 cup of coffee is $2.50.
Answer for screen readers
The cost of 1 cup of coffee is $c = 2.50$.
Steps to Solve
- Identify the system of equations
The given equations are: $$ c + 2d = 4.90 \quad (1) $$ $$ 2c + 3d = 8.60 \quad (2) $$
- Solve equation (1) for one variable
From equation (1), isolate $c$: $$ c = 4.90 - 2d $$
- Substitute into equation (2)
Replace $c$ in equation (2) with the expression found from equation (1): $$ 2(4.90 - 2d) + 3d = 8.60 $$
- Simplify the equation
Distribute and combine like terms: $$ 9.80 - 4d + 3d = 8.60 $$ $$ 9.80 - d = 8.60 $$
- Solve for $d$
Rearrange the equation to solve for $d$: $$ -d = 8.60 - 9.80 $$ $$ -d = -1.20 $$ $$ d = 1.20 $$
- Substitute $d$ back into equation (1)
Using the value of $d$ in equation (1) to find $c$: $$ c + 2(1.20) = 4.90 $$ $$ c + 2.40 = 4.90 $$
- Solve for $c$
Rearranging gives: $$ c = 4.90 - 2.40 $$ $$ c = 2.50 $$
The cost of 1 cup of coffee is $c = 2.50$.
More Information
The problem uses a system of linear equations to find the cost of coffee and doughnuts. It's a common method in algebra to determine unknowns based on known relationships.
Tips
- Failing to rearrange equations correctly when isolating variables.
- Miscalculating when substituting values back into equations.
- Forgetting to reduce or simplify terms properly during calculations.
