What is the correct way to multiply two matrices in Python, and what errors need to be fixed in the provided code?
Understand the Problem
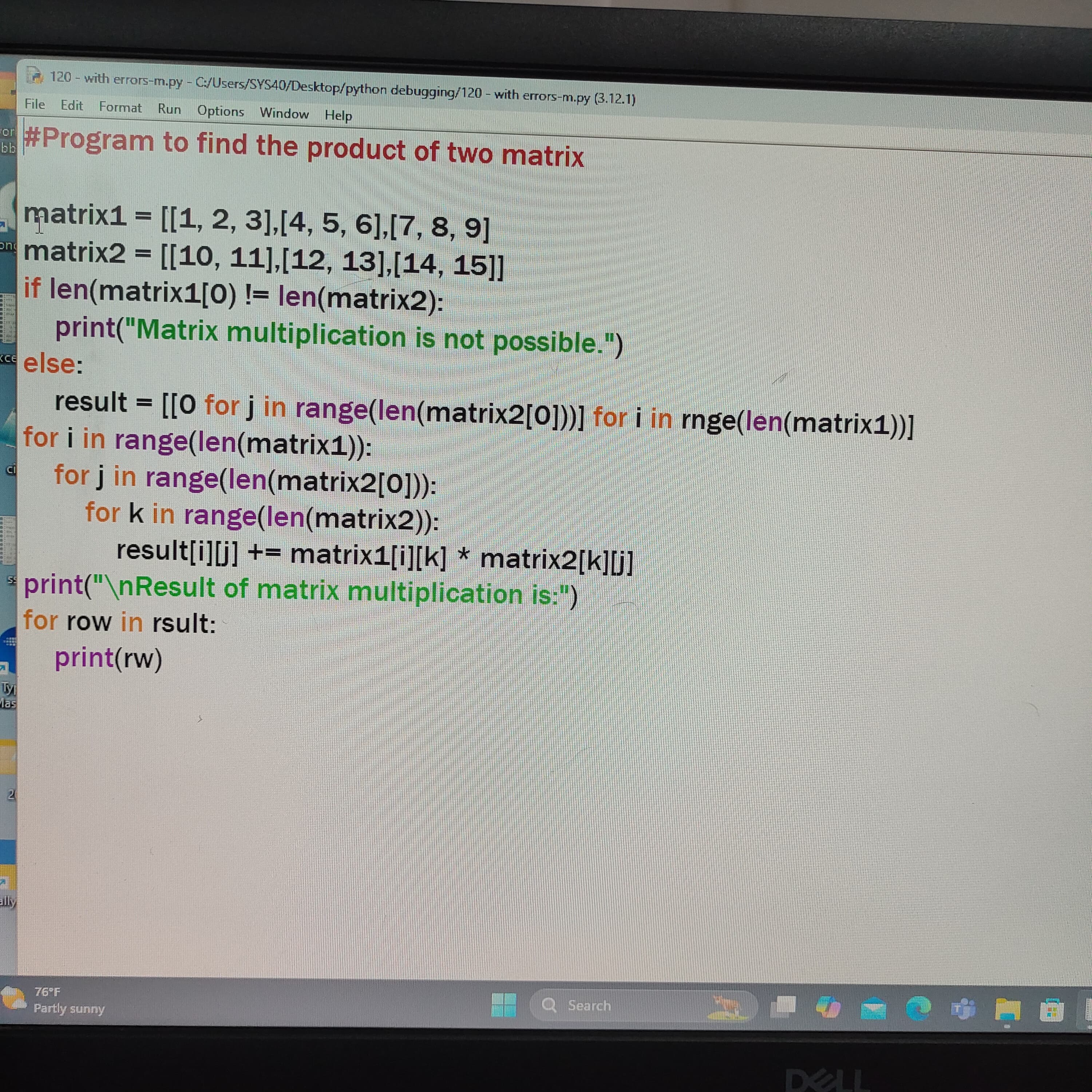
The question involves analyzing a Python program that attempts to multiply two matrices. It aims to identify and correct any errors in the code, particularly the syntax and logic for matrix multiplication.
Answer
Matrix multiplication is not possible.
Answer for screen readers
Matrix multiplication is not possible because the number of columns in matrix1 (3) does not match the number of rows in matrix2 (2).
Steps to Solve
-
Check Matrix Dimensions for Multiplication For matrix multiplication to be valid, the number of columns in the first matrix must equal the number of rows in the second matrix. Here,
matrix1has dimensions $3 \times 3$ (3 rows and 3 columns) andmatrix2has dimensions $2 \times 3$ (2 rows and 3 columns). Since $3 \neq 2$, matrix multiplication is not possible. -
Correct Logical Structure of Result Initialization In the original code, the
resultmatrix initialization is attempted but will ultimately be incorrect due to the first matrix's columns not matching the second matrix's rows. The correct initialization should follow the formula: $$ \text{result}[i][j] = 0 \text{ for } i=0...(\text{number of rows in matrix1}-1), j=0...(\text{number of columns in matrix2}-1) $$ -
Fix Nested Loop for Matrix Multiplication In a working implementation, the structure of the loops would generally follow this format:
for i in range(len(matrix1)):
for j in range(len(matrix2[0])):
for k in range(len(matrix2)):
result[i][j] += matrix1[i][k] * matrix2[k][j]
This ensures that each element of the resulting matrix is computed correctly.
- Output with Correct Variable Reference
The print statement should accurately reflect outputting each row of the final result. Instead of
print(rw), it should beprint(row)to correctly iterate over the list of results.
Matrix multiplication is not possible because the number of columns in matrix1 (3) does not match the number of rows in matrix2 (2).
More Information
Matrix multiplication requires that the matrices be conformable, meaning the number of columns in the first matrix must be equal to the number of rows in the second matrix. The dimension mismatch here prevents any valid multiplication.
Tips
- Forgetting to check the dimensions before attempting multiplication.
- Incorrect initialization of result matrix dimensions.
- Using incorrect variable names in print statements or result calculations.
AI-generated content may contain errors. Please verify critical information