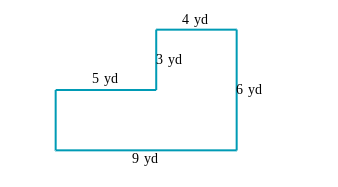
What is the area of the composite shape?
Understand the Problem
The question involves finding the area of a composite shape formed by different rectangles. We'll break down the shape into simpler components, calculate the area of each, and then sum those areas to find the total.
Answer
The total area is \( 54 \, \text{yd}^2 \).
Answer for screen readers
The total area of the composite shape is ( 54 , \text{yd}^2 ).
Steps to Solve
- Identify the Components of the Shape
The composite shape can be divided into two rectangles:
- Rectangle A (the larger one on the right)
- Rectangle B (the smaller one on the left)
- Calculate the Area of Rectangle A
For Rectangle A, the dimensions are:
- Width = 4 yd
- Height = 6 yd
The area of Rectangle A can be calculated using the formula for the area of a rectangle, which is: $$ \text{Area}_A = \text{Width} \times \text{Height} = 4 , \text{yd} \times 6 , \text{yd} $$
- Calculate the Area of Rectangle B
For Rectangle B, the dimensions are:
- Width = 9 yd
- Height = 5 yd
Using the same formula: $$ \text{Area}_B = \text{Width} \times \text{Height} = 9 , \text{yd} \times 5 , \text{yd} $$
- Sum the Areas of the Rectangles
Finally, add the areas of both rectangles to get the total area of the composite shape: $$ \text{Total Area} = \text{Area}_A + \text{Area}_B $$
The total area of the composite shape is ( 54 , \text{yd}^2 ).
More Information
The area of rectangles is a fundamental concept in geometry that helps in calculating the size of two-dimensional shapes. It's essential for various applications, including architecture, landscaping, and more.
Tips
- Forgetting to multiply the width and height correctly for each rectangle.
- Adding areas of rectangles in incorrect order or skipping one of the rectangles.
- Misreading dimensions from the diagram.
AI-generated content may contain errors. Please verify critical information