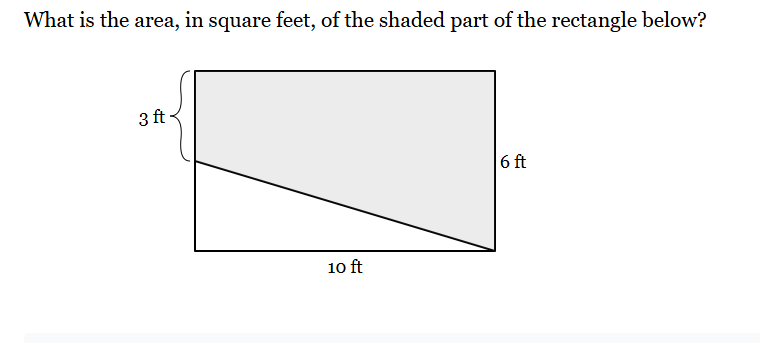
What is the area, in square feet, of the shaded part of the rectangle?
Understand the Problem
The question asks for the area of the shaded portion of a rectangle. The rectangle has dimensions 10 ft by 6 ft. A triangle is cut out of the rectangle. The height of the unshaded triangle is 3 ft. Thus we will need to calculate the area of the rectangle and subtract the area of the unshaded triangle to find the area of the shaded region.
Answer
$45 \text{ ft}^2$
Answer for screen readers
$45 \text{ ft}^2$
Steps to Solve
- Calculate the area of the rectangle
To find the area of the rectangle, multiply the length by the width. In this case, the length is 10 ft and the width is 6 ft. $$ Area_{rectangle} = length \times width = 10 \times 6 = 60 \text{ ft}^2 $$
- Calculate the height of the triangle
The height of the triangle is the height of the rectangle minus the 3ft given. $$ Height_{triangle} = 6 - 3 = 3 \text{ ft} $$
- Calculate the area of the triangle
The area of a triangle is given by $ \frac{1}{2} \times base \times height $. In this case, the base of the triangle is 10 ft and the height is 3 ft. $$ Area_{triangle} = \frac{1}{2} \times 10 \times 3 = \frac{30}{2} = 15 \text{ ft}^2 $$
- Calculate the area of the shaded region
Subtract the area of the triangle from the area of the rectangle to find the area of the shaded region. $$ Area_{shaded} = Area_{rectangle} - Area_{triangle} = 60 - 15 = 45 \text{ ft}^2 $$
$45 \text{ ft}^2$
More Information
The area of the shaded region is $45 \text{ ft}^2$.
Tips
A common mistake is forgetting to calculate the height of the triangle by subtracting 3 from the height of the rectangle (6 ft).
AI-generated content may contain errors. Please verify critical information