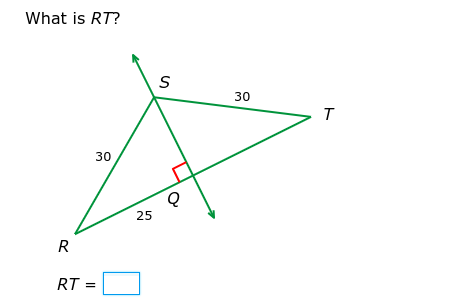
What is RT?
Understand the Problem
The question asks to find the distance of line RT. We can solve this using similar triangles and the Pythagorean theorem.
Answer
$RT = 36$
Answer for screen readers
$RT = 36$
Steps to Solve
- Find the length of $SQ$ using the Pythagorean theorem.
In right triangle $RQS$, we have $RQ = 25$ and $RS = 30$. We can find $SQ$ using the Pythagorean theorem: $RS^2 = RQ^2 + SQ^2$. $$30^2 = 25^2 + SQ^2$$ $$900 = 625 + SQ^2$$ $$SQ^2 = 275$$ $$SQ = \sqrt{275} = 5\sqrt{11}$$
- Notice that triangles $RQS$ and $TSQ$ are similar.
$\angle RQS$ and $\angle TSQ$ are right angles. Also, $\angle RSQ$ and $\angle QST$ must be equal. So, the triangles are similar.
- Write a proportion to find $QT$.
Since $\triangle RQS \sim \triangle TSQ$, we can write the proportion: $$\frac{RQ}{SQ} = \frac{SQ}{QT}$$ Substitute the known values: $$\frac{25}{5\sqrt{11}} = \frac{5\sqrt{11}}{QT}$$ Solve for $QT$: $$25 \cdot QT = (5\sqrt{11})^2$$ $$25 \cdot QT = 25 \cdot 11$$ $$QT = 11$$
- Find $RT$ by adding $RQ$ and $QT$.
$RT = RQ + QT = 25 + 11 = 36$
$RT = 36$
More Information
The problem involves similar triangles and the Pythagorean theorem. Identifying the similar triangles is crucial for setting up the correct proportions.
Tips
A common mistake is failing to correctly identify the corresponding sides in similar triangles, leading to an incorrect proportion. Another mistake is to incorrectly compute $SQ$ using the Pythagorean theorem.
AI-generated content may contain errors. Please verify critical information