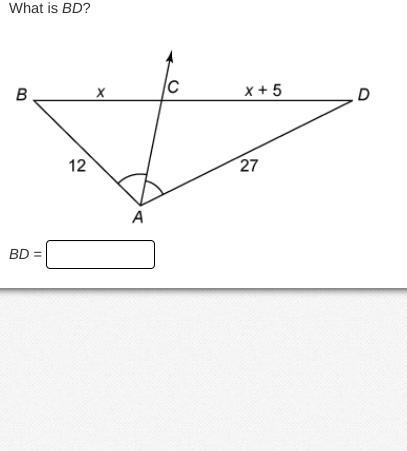
What is BD?

Steps to Solve

1. Identify the angles in triangle ABC
   Since angle A is a right angle (90 degrees), we can apply the Pythagorean theorem to find the lengths of segments AC and AB. The lengths are given as:

   • AC = 12
   • AB = x

2. Set up the equation using the Pythagorean theorem
   According to the Pythagorean theorem:
   $$ AC^2 + AB^2 = BC^2 $$
   Substituting the known values, we have:
   $$ 12^2 + x^2 = BC^2 $$
   Which simplifies to:
   $$ 144 + x^2 = BC^2 $$

3. Set up the equation for length BD using segment CD
   The length CD is given as ( x + 5 ) and the length AD is given as 27. Knowing BD = BC + CD, we can express BD in terms of x:
   $$ BD = BC + (x + 5) $$

4. Express BD in terms of x
   Since we've established that ( BC = \sqrt{144 + x^2} ), we can substitute:
   $$ BD = \sqrt{144 + x^2} + (x + 5) $$

5. Set the equation for AD
   Since AD = BD and AD = 27, we set up the equation:
   $$ \sqrt{144 + x^2} + (x + 5) = 27 $$

6. Solve for x
   Rearranging gives:
   $$ \sqrt{144 + x^2} = 27 - (x + 5) $$
   Simplifying results in:
   $$ \sqrt{144 + x^2} = 22 - x $$

   Now, square both sides:
   $$ 144 + x^2 = (22 - x)^2 $$
   Expanding the right side:
   $$ 144 + x^2 = 484 - 44x + x^2 $$

7. Simplify and solve for x
   By cancelling ( x^2 ) from both sides:
   $$ 144 = 484 - 44x $$
   Rearranging gives:
   $$ 44x = 484 - 144 $$
   $$ 44x = 340 $$
   $$ x = \frac{340}{44} = \frac{85}{11} \approx 7.73$$

8. Find the length of segment BD
   Now that we have ( x ), we compute ( BD ):
   $$ BD = \sqrt{144 + \left(\frac{85}{11}\right)^2} + \left(\frac{85}{11} + 5\right) $$

   Solve for ( BD ).