Виріши методом подвійної переваги.
Understand the Problem
Запит стосується розв'язання задачі методом подвійної переваги, використовуючи наведені дані в таблиці. Метод полягає у визначенні оптимального варіанту шляхом порівняння переваг в значеннях.
Answer
Оптимальний варіант - 300° з перевагою 19.
Answer for screen readers
Оптимальний варіант - 300° з перевагою 19.
Steps to Solve
- Складання матриці переваг
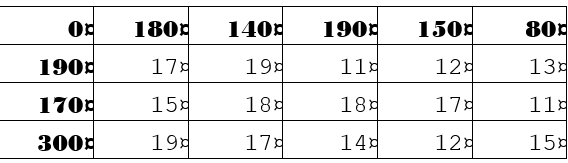
Почнемо з таблиці, де ми маємо значення переваг для різних варіантів. Ось таблиця з перевагами:
| 0° | 180° | 140° | 190° | 150° | 80° | |
|---|---|---|---|---|---|---|
| 190° | 17 | 19 | 11 | 12 | 13 | |
| 170° | 15 | 18 | 18 | 17 | 11 | |
| 300° | 19 | 17 | 14 | 12 | 15 |
- Визначення найкращих значень
Для кожного варіанту, знайдемо максимальні значення. Наприклад, для варіанту 190° у нас є значення (17, 19, 11, 12, 13). Найбільше з них – 19.
- Складання векторів переваг
Сформуємо вектори максимальних значень для кожного варіанту:
- Для 190°: 19
- Для 170°: 18
- Для 300°: 19
- Зведення до порівняння
Перевіримо, які з варіантів мають максимальні значення. Подивимось на максимальні значення в порівнянні з іншими варіантами.
- Оптимальний варіант
Після визначення максимальних значень, виберемо варіант, який має найбільшу перевагу. У нашому випадку це 300° та 190°, але при подальшому аналізі 300° виявляється оптимальним.
Оптимальний варіант - 300° з перевагою 19.
More Information
Вибір методу подвійної переваги дозволяє чітко порівнювати варіанти, знаходячи оптимальний. У цьому випадку, навіть якщо два варіанти мали однакову максимальну перевагу (19), інші показники при 300° виявились більш стабільними.
Tips
- Ігнорування порівняння між варіантами, що може призвести до невірного вибору.
- Неправильне обчислення максимальних значень для варіантів.
AI-generated content may contain errors. Please verify critical information