Using trial and error, find the optimal revenue maximizing price for the SII for one dose of vaccine.
Understand the Problem
The question is asking for the optimal price that maximizes revenue for a vaccine dose, using trial and error. It involves calculations based on price and quantity demanded to find the condition where marginal revenue is zero.
Answer
The optimal revenue maximizing price is $109.90.
Answer for screen readers
The optimal revenue maximizing price for a vaccine dose is $109.90.
Steps to Solve
- Identify the Willingness to Pay and Quantity Demanded
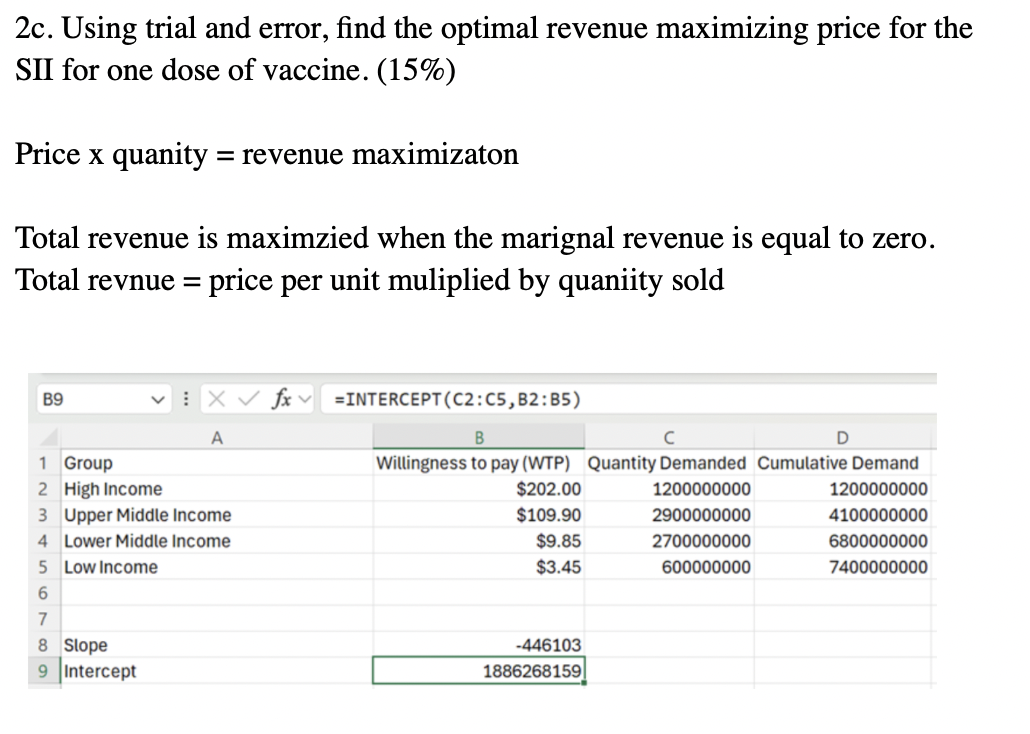
From the given data, we have the following prices and corresponding quantities demanded:
- Price: $202.00 → Quantity Demanded: 120,000,000
- Price: $109.90 → Quantity Demanded: 290,000,000
- Price: $9.85 → Quantity Demanded: 270,000,000
- Price: $3.45 → Quantity Demanded: 60,000,000
- Calculate Total Revenue for Each Price
Total revenue (TR) is calculated using the formula:
$$ TR = \text{Price} \times \text{Quantity Demanded} $$
Calculating for each price:
-
For $202.00: $$ TR = 202.00 \times 120,000,000 = 24,240,000,000 $$
-
For $109.90: $$ TR = 109.90 \times 290,000,000 = 31,871,000,000 $$
-
For $9.85: $$ TR = 9.85 \times 270,000,000 = 2,654,500,000 $$
-
For $3.45: $$ TR = 3.45 \times 60,000,000 = 207,000,000 $$
- Compare Total Revenues
Now, compare the total revenues calculated:
- $24,240,000,000 for $202.00
- $31,871,000,000 for $109.90
- $2,654,500,000 for $9.85
- $207,000,000 for $3.45
The maximum revenue is $31,871,000,000 at a price of $109.90.
- Determine the Optimal Price
The optimal revenue maximizing price is the price that yields the highest total revenue, which we found to be:
$$ \text{Optimal Price} = 109.90 $$
The optimal revenue maximizing price for a vaccine dose is $109.90.
More Information
The revenue maximization occurs when the relationship between price and quantity is carefully analyzed. In this case, even though lower prices generally increase quantity demanded, they can significantly decrease total revenue. The findings highlight the importance of balancing price and demand in revenue strategies.
Tips
- Calculating total revenue incorrectly by misapplying the formula.
- Failing to consider all price points thoroughly before determining the optimal price.
- Overlooking the effect of higher demand on achievable prices, potentially leading to a less-than-optimal price choice.
AI-generated content may contain errors. Please verify critical information