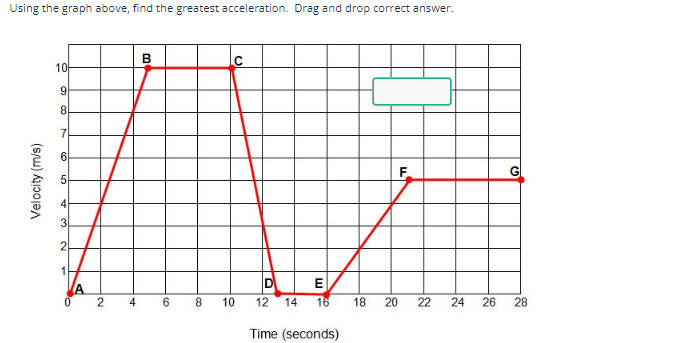
Using the graph above, find the greatest acceleration.

Steps to Solve

1. Identify Key Points on the Graph Locate the points A, B, C, D, E, F, and G on the velocity vs. time graph. These points help us determine the changes in velocity.

2. Calculate the Slope (Acceleration) Between Points Acceleration is defined as the change in velocity ($\Delta v$) divided by the change in time ($\Delta t$). We calculate the slope between each segment of the graph:

   • Between points A and B:

     • $\Delta v = v_B - v_A = 10 - 0 = 10 , \text{m/s}$
     • $\Delta t = t_B - t_A = 4 - 0 = 4 , \text{s}$
     • Acceleration = $\frac{10 , \text{m/s}}{4 , \text{s}} = 2.5 , \text{m/s}^2$

   • Between points C and D:

     • $\Delta v = v_D - v_C = 0 - 10 = -10 , \text{m/s}$
     • $\Delta t = t_D - t_C = 12 - 10 = 2 , \text{s}$
     • Acceleration = $\frac{-10 , \text{m/s}}{2 , \text{s}} = -5 , \text{m/s}^2$

   • Between points E and F:

     • $\Delta v = v_F - v_E = 5 - 0 = 5 , \text{m/s}$
     • $\Delta t = t_F - t_E = 16 - 12 = 4 , \text{s}$
     • Acceleration = $\frac{5 , \text{m/s}}{4 , \text{s}} = 1.25 , \text{m/s}^2$

3. Find the Greatest Acceleration Compare the calculated accelerations:

   • A to B: $2.5 , \text{m/s}^2$
   • C to D: $-5 , \text{m/s}^2$
   • E to F: $1.25 , \text{m/s}^2$

   The greatest acceleration is $2.5 , \text{m/s}^2$.