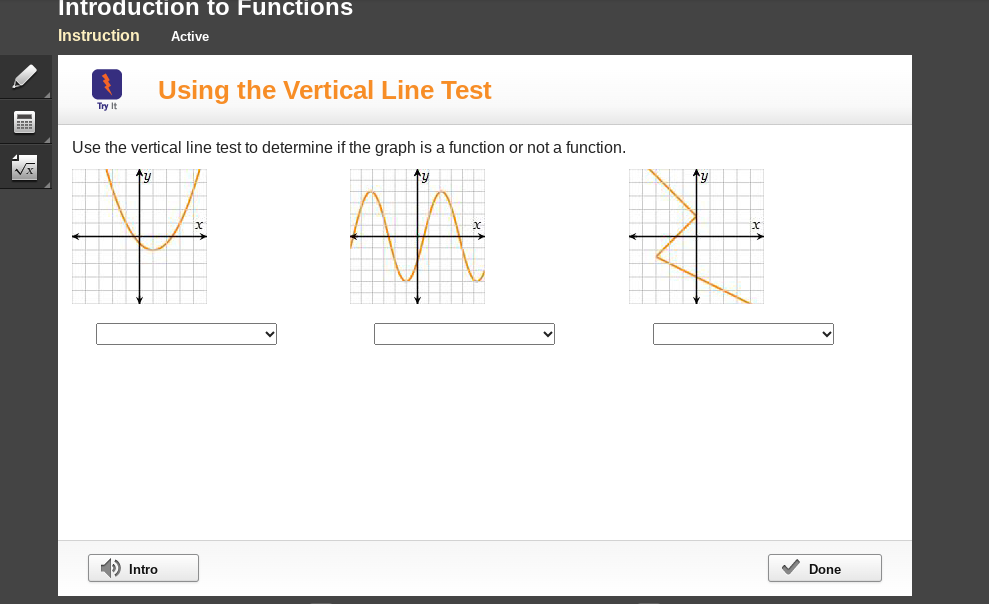
Use the vertical line test to determine if the graph is a function or not.
Understand the Problem
The question is asking to use the vertical line test to determine if each graph represents a function or not. The vertical line test states that if a vertical line intersects the graph at more than one point, then the graph is not a function.
Answer
First graph: Not a function; Second graph: Not a function; Third graph: Function.
Answer for screen readers
- First graph: Not a function
- Second graph: Not a function
- Third graph: Function
Steps to Solve
-
Analyze the first graph Examine the first graph visually. Draw vertical lines at various x-values. If you can draw a vertical line that intersects the graph at more than one point, it fails the vertical line test.
-
Evaluate the second graph Look at the second graph in the same way. Draw vertical lines through different x-values and check for intersections. If any vertical line touches the graph at two points, then this graph is not a function.
-
Check the third graph Now, move to the third graph and apply the vertical line test. Again, if a vertical line can intersect the graph at multiple points, it fails the test, indicating it is not a function.
-
Record the results Based on the tests performed, categorize each graph as either a function or not a function. The result should be inputted into the provided dropdown menus.
- First graph: Not a function
- Second graph: Not a function
- Third graph: Function
More Information
The vertical line test is a quick way to determine if a relation is a function. In this case, both the first and second graphs show multiple intersections with vertical lines, indicating that they do not meet the criteria of a function. The third graph does not show multiple intersections, confirming it is indeed a function.
Tips
- Miscounting intersections: It's important to carefully check each potential intersection point.
- Assuming wavy lines or curves are functions without checking intersections: Always use the vertical line test for confirmation, even for curves.
AI-generated content may contain errors. Please verify critical information