Use the Squeeze Theorem to evaluate the following limit: $\lim_{x\to -4^+} \frac{\sin(\frac{1}{x+4})}{\ln(3x+12)}$
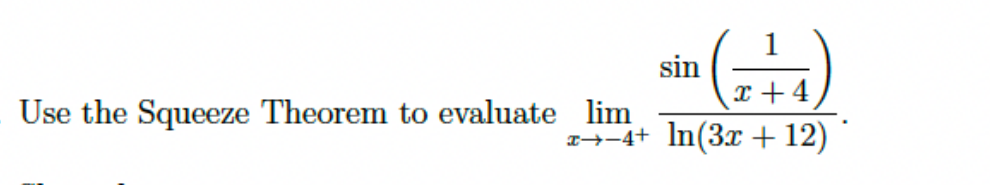
Understand the Problem
The question asks us to find the limit of the given function. The function contains a sine function, a logarithmic function, and a rational expression. We must use the Squeeze Theorem to find the limit as x approaches -4 from the right.
Answer
0
Answer for screen readers
0
Steps to Solve
- Bound the sine function
The sine function is always between -1 and 1, so we have: $$-1 \le \sin\left(\frac{1}{x+4}\right) \le 1$$
- Divide by the logarithmic function
Divide all sides of the inequality by $\ln(3x+12)$. Since $x \to -4^+$, then $x > -4$, so $3x > -12$ and $3x + 12 > 0$. As $x \to -4^+$, $3x+12 \to 0^+$, and hence $\ln(3x+12) \to -\infty$. Since we are dividing by a negative quantity, we must flip the inequality signs: $$\frac{-1}{\ln(3x+12)} \ge \frac{\sin\left(\frac{1}{x+4}\right)}{\ln(3x+12)} \ge \frac{1}{\ln(3x+12)}$$
- Evaluate the limits of the bounding functions
Now we take the limit as $x \to -4^+$ of the two bounding functions:
$$\lim_{x \to -4^+} \frac{-1}{\ln(3x+12)} = 0$$ and $$\lim_{x \to -4^+} \frac{1}{\ln(3x+12)} = 0$$
Since $\lim_{x\to -4^+} 3x+12 = 0^+$, $\lim_{x\to -4^+} \ln(3x+12) = -\infty$. Therefore, the fractions go to $0$.
- Apply the Squeeze Theorem
Since both bounding functions have a limit of 0 as $x \to -4^+$, by the Squeeze Theorem, the limit of the function in the middle must also be 0: $$\lim_{x \to -4^+} \frac{\sin\left(\frac{1}{x+4}\right)}{\ln(3x+12)} = 0$$
0
More Information
The Squeeze Theorem allows us to find the limit of a function by bounding it between two other functions whose limits are known and equal.
Tips
A common mistake is to not realize that $\ln(3x+12)$ goes to $-\infty$ as $x \to -4^+$, making both bounding fractions tend to $0$. Also, failing to consider that $\ln(3x+12)$ is negative and flipping the inequalities can lead to an incorrect result.
AI-generated content may contain errors. Please verify critical information