Use the sentence $x^2 + \frac{1}{x^2} = 5$ to evaluate the expression $(x + \frac{1}{x})^2$.
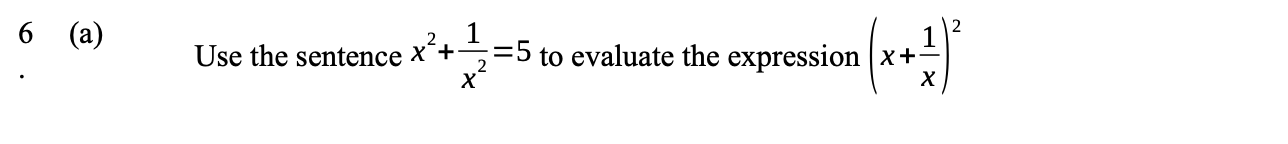
Understand the Problem
The question is asking to evaluate the expression $(x + \frac{1}{x})^2$ given that $x^2 + \frac{1}{x^2} = 5$. We need to manipulate the given equation to find the value of the expression.
Answer
7
Answer for screen readers
7
Steps to Solve
- Expand the expression Expand the expression $(x + \frac{1}{x})^2$ using the formula $(a+b)^2 = a^2 + 2ab + b^2$.
$(x + \frac{1}{x})^2 = x^2 + 2(x)(\frac{1}{x}) + (\frac{1}{x})^2 = x^2 + 2 + \frac{1}{x^2}$
- Rearrange the expanded expression Rearrange the expanded expression to group the terms $x^2$ and $\frac{1}{x^2}$ together.
$x^2 + 2 + \frac{1}{x^2} = x^2 + \frac{1}{x^2} + 2$
- Substitute the given value Substitute the given value $x^2 + \frac{1}{x^2} = 5$ into the rearranged expression.
$x^2 + \frac{1}{x^2} + 2 = 5 + 2$
- Evaluate the expression Evaluate the expression to find the final value.
$5 + 2 = 7$
7
More Information
The problem uses algebraic manipulation to find the value of an expression indirectly, without needing to solve for the variable $x$.
Tips
A common mistake is incorrectly expanding the square of the binomial. Remember that $(a+b)^2 = a^2 + 2ab + b^2$, not $a^2 + b^2$. Another common mistake is not recognizing that $2(x)(\frac{1}{x}) = 2$.
AI-generated content may contain errors. Please verify critical information