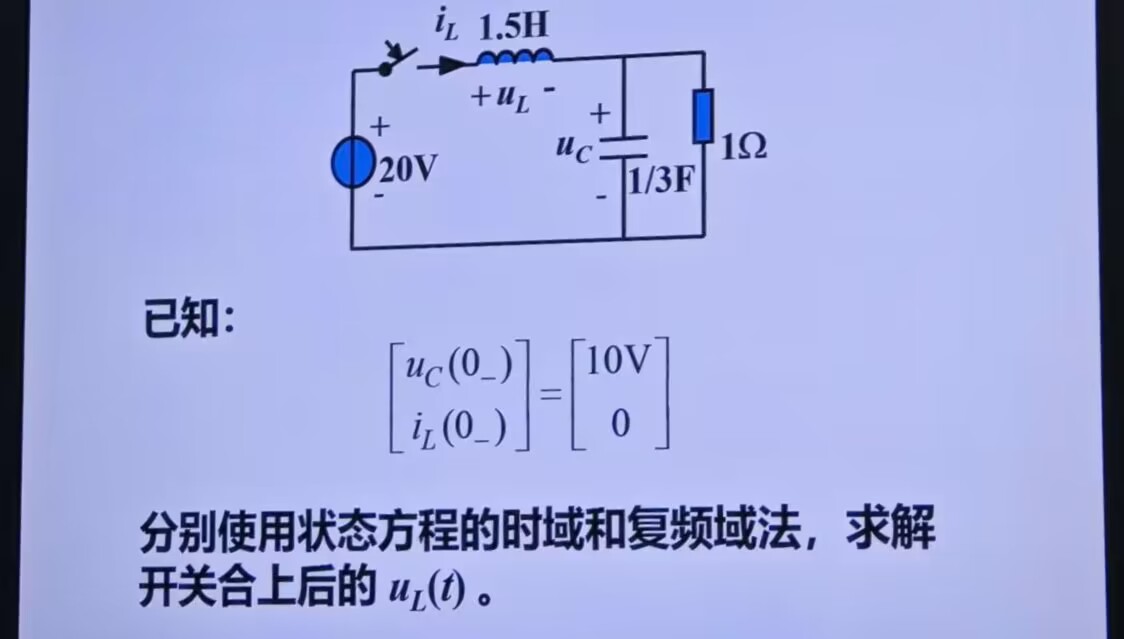
分别使用状态方程的时域和频域法，求解开关合上的电流ul(t)。

Steps to Solve

1. 建立状态方程 根据电路图，开关断开后，电压 $u_C$ 和电流 $i_L$ 可以被描述为状态变量。状态方程如下： $$ \begin{bmatrix} \dot{u}_C \ \dot{i}_L \end{bmatrix} = \begin{bmatrix} -\frac{1}{C} & -\frac{1}{L} \ \frac{1}{L} & -\frac{R}{L} \end{bmatrix} \begin{bmatrix} u_C \ i_L \end{bmatrix}

\begin{bmatrix} 0 \ \frac{1}{L} \end{bmatrix} u_s $$ 这里 $u_s = 20V$，$R = 1\Omega$，$L = 1.5H$，$C = \frac{1}{3}F$。

2. 定义矩阵和常数 将已知的值代入状态方程的系数矩阵，得到： $$ A = \begin{bmatrix} -3 & -\frac{2}{3} \ \frac{2}{3} & -\frac{2}{3} \end{bmatrix} $$ 和输入矩阵： $$ B = \begin{bmatrix} 0 \ \frac{2}{3} \end{bmatrix} $$

3. 分析初始条件 初始条件为： $$ \begin{bmatrix} u_C(0) \ i_L(0) \end{bmatrix} = \begin{bmatrix} 10 \ 0 \end{bmatrix} $$

4. 求解特征方程 特征方程为 $|A - \lambda I| = 0$，求解 $A$ 的特征值。计算特征值可得： $$ \lambda^2 + \frac{4}{3}\lambda + 2 = 0 $$ 使用求根公式： $$ \lambda_{1,2} = \frac{-\frac{4}{3} \pm \sqrt{(\frac{4}{3})^2 - 4 \cdot 2}}{2} \ = \frac{-\frac{4}{3} \pm \sqrt{\frac{16}{9} - 8}}{2} $$

5. 求解系统响应 利用拉普拉斯变换技术进行求解，得到系统的时域响应： $$ u_L(t) = \mathcal{L}^{-1}\left{\frac{U_L(s)}{s+\lambda}\right} $$ 代入具体数值，通过反变换求出 $u_L(t)$。