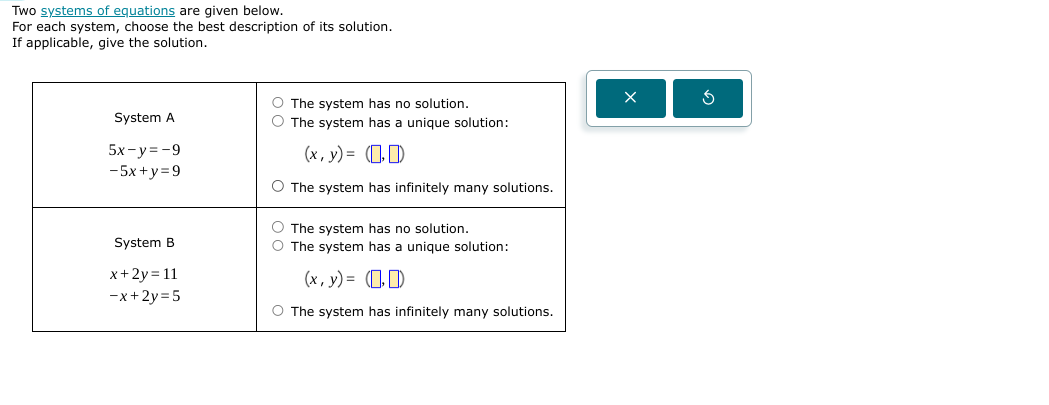
Two systems of equations are given below. For each system, choose the best description of its solution. If applicable, give the solution.

Understand the Problem

The question presents two systems of linear equations and asks for the best description of the solutions for each system, including whether they have no solution, a unique solution, or infinitely many solutions.

Answer

- System A: infinitely many solutions - System B: unique solution $ (3, 4) $

Steps to Solve

Identify the equations in System A
The equations are:
$$ 5x - y = -9 $$
$$ -5x + y = 9 $$
Analyze System A
We can add the two equations together to eliminate (y):
$$ (5x - y) + (-5x + y) = -9 + 9 $$
This simplifies to:
$$ 0 = 0 $$
Since this is a true statement, it indicates that the two equations represent the same line. Thus, there are infinitely many solutions.
Identify the equations in System B
The equations are:
$$ x + 2y = 11 $$
$$ -x + 2y = 5 $$
Analyze System B
We can add the two equations to eliminate (x):
$$ (x + 2y) + (-x + 2y) = 11 + 5 $$
This simplifies to:
$$ 4y = 16 $$
Solving for (y) gives:
$$ y = 4 $$
Now, substitute this value back into one of the original equations to find (x):
$$ x + 2(4) = 11 $$
$$ x + 8 = 11 $$
$$ x = 3 $$
Thus, the solution for System B is ( (3, 4) ), which means it has a unique solution.

System A has infinitely many solutions.
System B has a unique solution: ( (3, 4) ).

More Information

Both systems of equations illustrate different scenarios in solving linear equations: System A represents dependent equations leading to infinitely many solutions, while System B represents independent equations resulting in a single unique intersection point.

Tips

Confusing dependent equations (which have infinitely many solutions) with inconsistent equations (which have no solutions).
Forgetting to substitute the found variable back into one of the original equations after solving for another variable.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!