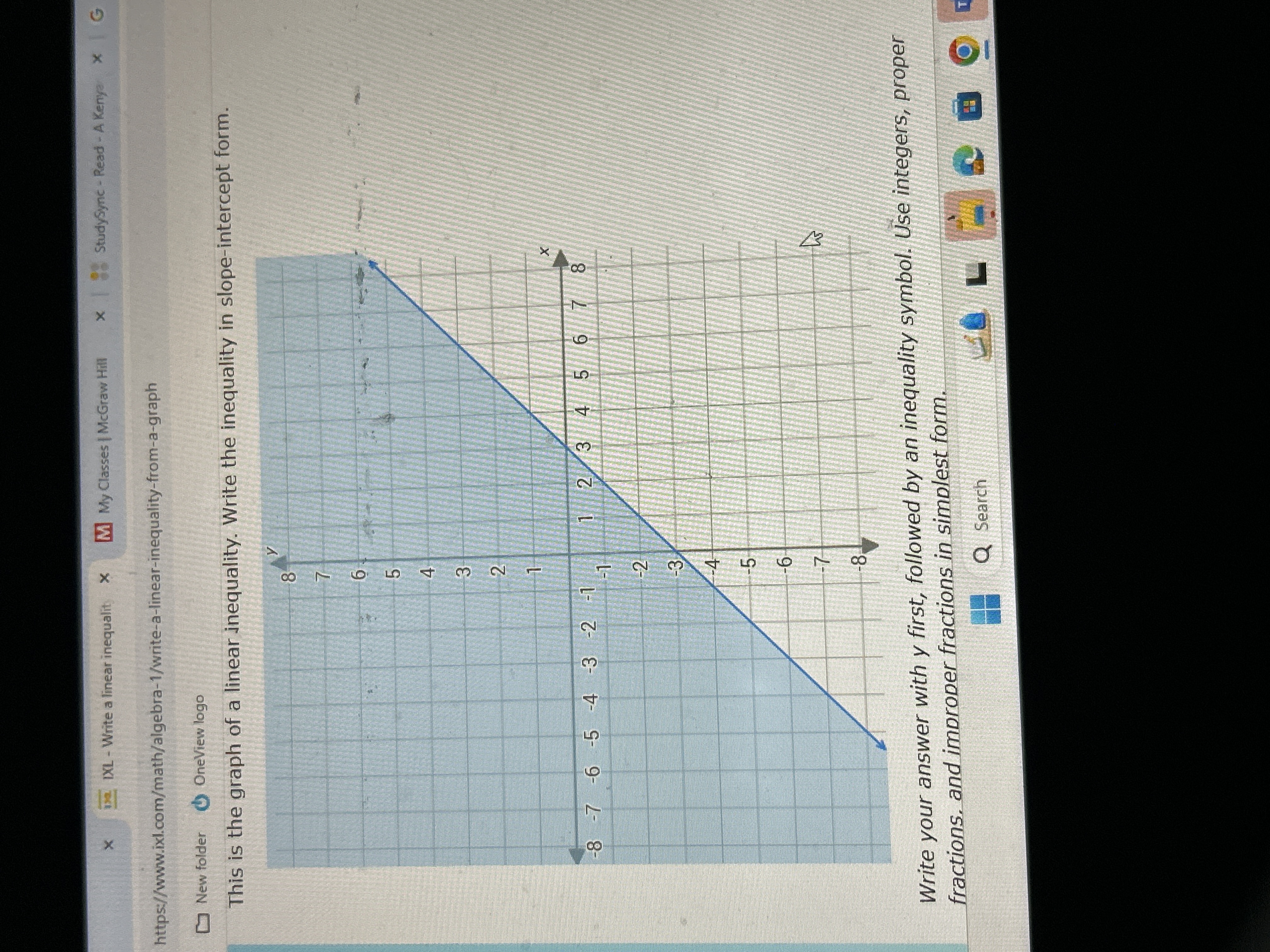
This is the graph of a linear inequality. Write the inequality in slope-intercept form.
Understand the Problem
The question is asking for the linear inequality represented by the graph in slope-intercept form (y = mx + b), including the inequality symbol that indicates whether the relationship is greater than or less than.
Answer
The inequality is: $$ y > x + 2 $$
Answer for screen readers
The linear inequality represented by the graph in slope-intercept form is:
$$ y > x + 2 $$
Steps to Solve
-
Identify the slope and y-intercept
From the graph, determine the slope ($m$) and y-intercept ($b$). The y-intercept is the point where the line intersects the y-axis, which in this case is at $(0, 2)$. The slope can be found by identifying two points on the line. For example, from $(2, 4)$ to $(4, 6)$, the change in $y$ is $6 - 4 = 2$ and the change in $x$ is $4 - 2 = 2$, giving a slope of $m = \frac{2}{2} = 1$. -
Write the equation in slope-intercept form
The slope-intercept form is written as $y = mx + b$. Substituting the slope and the y-intercept, the equation becomes:
$$ y = 1x + 2 $$
which simplifies to
$$ y = x + 2 $$ -
Determine the inequality symbol
The line represented in the graph is dashed, indicating that the values on the line are not included in the solution set. Since the shaded region is above the line, the inequality symbol will be “greater than.” Therefore, the inequality is:
$$ y > x + 2 $$
The linear inequality represented by the graph in slope-intercept form is:
$$ y > x + 2 $$
More Information
The dashed line indicates that the points on the line are not included in the solution, meaning it’s a strict inequality (greater than or less than) rather than greater than or equal to or less than or equal to. The slope of 1 indicates that for each increase of 1 in $x$, $y$ increases by 1.
Tips
- Ignoring the dashed line: A common mistake is assuming that the line includes the points on it, which leads to using $\geq$ or $\leq$ instead of $>$ or $<$.
- Incorrectly identifying slope: Ensure that the rise over run calculation for slope is accurate by selecting two clear points on the line.
AI-generated content may contain errors. Please verify critical information