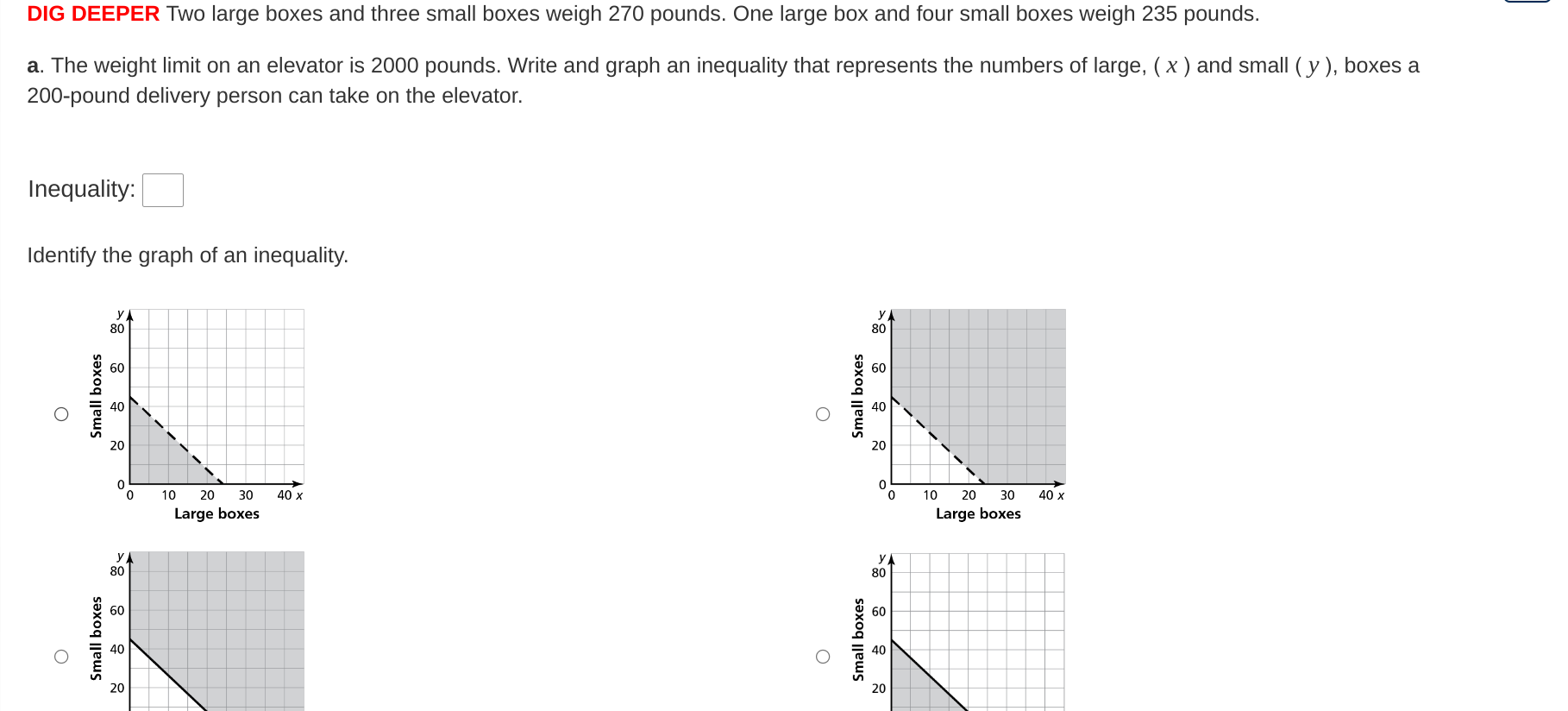
The weight limit on an elevator is 2000 pounds. Write and graph an inequality that represents the numbers of large (x) and small (y) boxes a 200-pound delivery person can take on t... The weight limit on an elevator is 2000 pounds. Write and graph an inequality that represents the numbers of large (x) and small (y) boxes a 200-pound delivery person can take on the elevator. Read more

Steps to Solve

1. Determine the weight of large and small boxes

First, we need to find the weight of one large box and one small box from the provided information. We have two equations from the weights:

• For two large boxes and three small boxes: $$ 2L + 3S = 270 $$

• For one large box and four small boxes: $$ L + 4S = 235 $$

2. Solve the equations simultaneously

To solve for the weights (L) (large box) and (S) (small box), we can express (L) from the second equation:

$$ L = 235 - 4S $$

Substituting (L) into the first equation gives:

$$ 2(235 - 4S) + 3S = 270 $$

3. Simplify the equation

Now distribute and simplify the equation:

$$ 470 - 8S + 3S = 270 $$

Combine like terms:

$$ 470 - 5S = 270 $$

4. Isolate (S)

Rearrange the equation to solve for (S):

$$ -5S = 270 - 470 \ -5S = -200 \ S = 40 $$

5. Substitute back to find (L)

Now substitute (S) back into the equation for (L):

$$ L = 235 - 4(40) \ L = 235 - 160 \ L = 75 $$

6. Write the inequality for elevator weight limit

The inequality needs to consider the weight of the delivery person as well. The weight limit is 2000 pounds, so we have:

$$ 200 + 75x + 40y \leq 2000 $$

Subtract 200 from both sides:

$$ 75x + 40y \leq 1800 $$

7. Graph the inequality

To graph the inequality, first find the intercepts by setting (x) and (y) to zero:

• Set (x = 0): $$ 40y \leq 1800 \ y \leq 45 $$ So, the y-intercept is (0, 45).

• Set (y = 0): $$ 75x \leq 1800 \ x \leq 24 $$ So, the x-intercept is (24, 0).

Now plot these points on a graph and shade below the line formed by the equation $75x + 40y = 1800$.