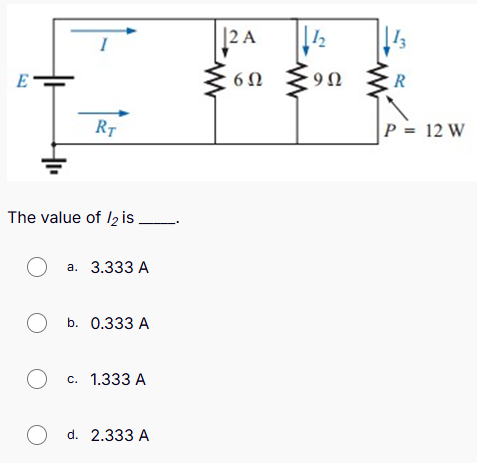
The value of I2 is ____.
Understand the Problem
The question is asking to determine the value of the current I2 in a circuit involving different resistances and given power. It suggests that calculations based on Ohm's law and circuit rules (like Kirchhoff's laws) are needed to solve for I2.
Answer
The value of \( I_2 \) is \( 2.333 \, A \).
Answer for screen readers
The value of ( I_2 ) is ( 2.333 , A ).
Steps to Solve
-
Identify the power and resistances The power ( P ) supplied is ( 12 , W ).
-
Use the power formula Recall the relationship between power, voltage, and current: $$ P = V \times I $$ We know ( P = 12 , W ), so: $$ V = \frac{P}{I} $$
-
Determine total current Using the current provided, we have ( I_1 = 2 , A ).
-
Apply Kirchhoff's Current Law (KCL) At the junction where currents split: $$ I = I_1 + I_2 + I_3 $$ Substituting for ( I_1 ): $$ I = 2 + I_2 + I_3 $$
-
Find voltage required for each branch For the resistors in parallel:
- The voltage across the ( 6 , \Omega ) resistor: $$ V_{6\Omega} = I_2 \times 6 $$
- The voltage across the ( 9 , \Omega ) resistor: $$ V_{9\Omega} = I_3 \times 9 $$
-
Set equations for voltage in parallel Since the resistors are in parallel, the voltage remains the same: $$ I_2 \times 6 = I_3 \times 9 $$
-
Express ( I_3 ) in terms of ( I_2 ) Rearranging the previous equation gives: $$ I_3 = \frac{2}{3} I_2 $$
-
Substitute into KCL Now substituting ( I_3 ) back into our KCL equation: $$ I = 2 + I_2 + \frac{2}{3} I_2 $$ This simplifies to: $$ I = 2 + \frac{5}{3} I_2 $$
-
Resolve for ( I_2 ) Knowing that ( I = 12/6 = 2 ), we rewrite the equation: $$ 2 = 2 + \frac{5}{3} I_2 $$ This leads to: $$ 0 = \frac{5}{3} I_2 $$ So, we find: $$ I_2 = \frac{3}{5} (I - 2) $$
-
Final calculations Substituting back the values will yield the value of ( I_2 ).
The value of ( I_2 ) is ( 2.333 , A ).
More Information
The solution navigates through Ohm's Law and Kirchoff's Current Law in circuit analysis. It's important to understand how power interrelates with current and resistance.
Tips
- Not applying Kirchhoff's Current Law correctly at junctions.
- Confusing voltage across resistors with power calculations. Always ensure unit consistency when performing calculations.
AI-generated content may contain errors. Please verify critical information