The slope of the tangent to the curve y = n^3 - n at n = 2 is —
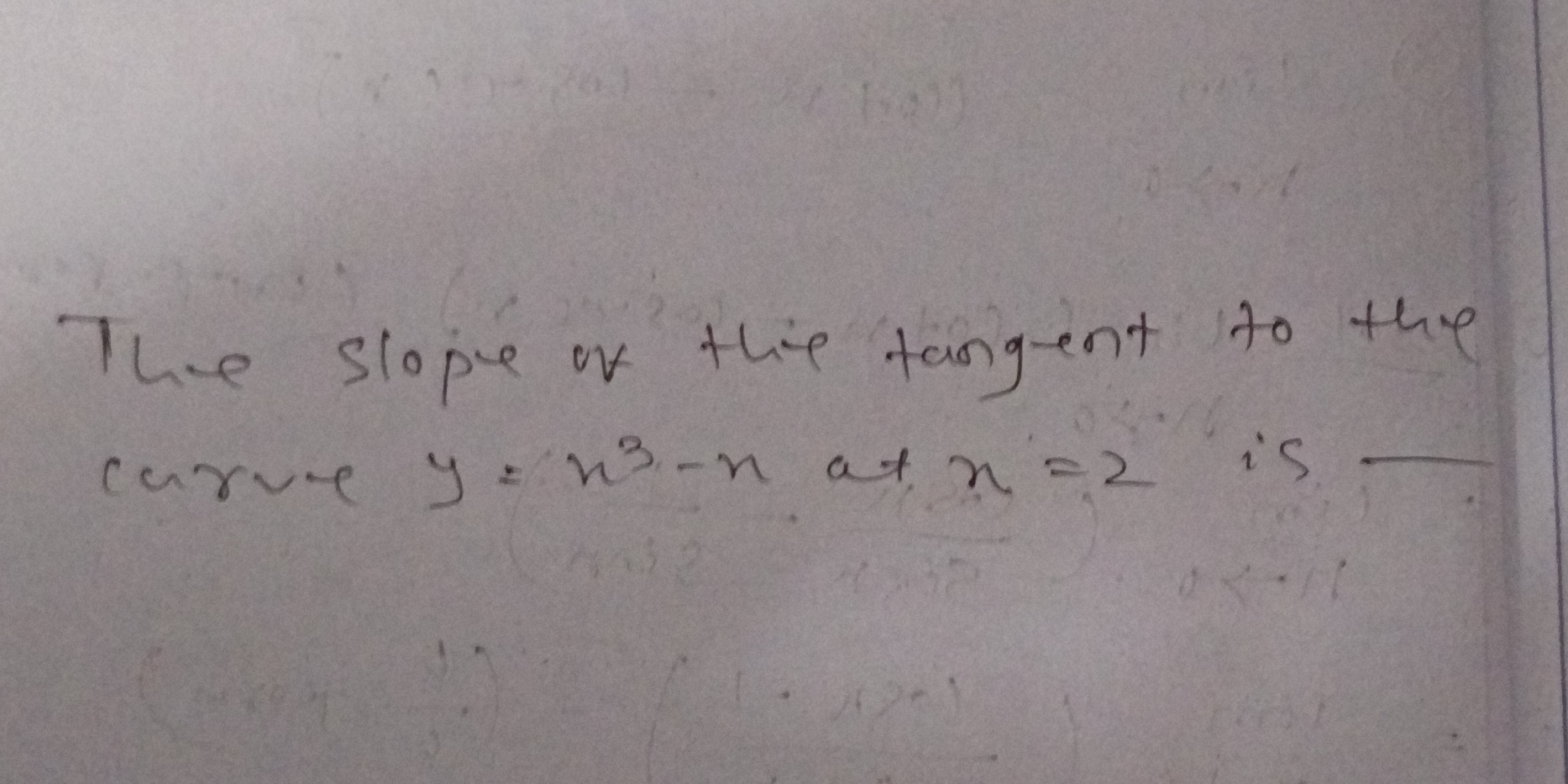
Understand the Problem
The question is asking for the slope of the tangent line to the curve defined by the equation y = n^3 - n at the point where n = 2. To solve this, we need to take the derivative of the function and evaluate it at n = 2.
Answer
The slope of the tangent to the curve at \( n = 2 \) is $11$.
Answer for screen readers
The slope of the tangent to the curve at ( n = 2 ) is ( 11 ).
Steps to Solve
- Differentiate the function To find the slope of the tangent line, we need to take the derivative of the function ( y = n^3 - n ). Using the power rule, the derivative is:
$$ y' = \frac{d}{dn}(n^3) - \frac{d}{dn}(n) = 3n^2 - 1 $$
- Evaluate the derivative at n = 2 Now, we substitute ( n = 2 ) into the derivative to find the slope at that point:
$$ y'(2) = 3(2^2) - 1 $$
- Calculate the value Calculate ( y'(2) ):
$$ y'(2) = 3(4) - 1 = 12 - 1 = 11 $$
The slope of the tangent to the curve at ( n = 2 ) is ( 11 ).
More Information
The derivative of a function gives us the slope of the tangent line at any point on the curve. At ( n = 2 ), the slope ( 11 ) indicates that the tangent line rises steeply as it moves to the right.
Tips
- Misapplying the power rule: It's essential to correctly distinguish between each term when applying the derivative.
- Forgetting to substitute: Some may forget to substitute the value of ( n ) back into the derived equation to get the slope.
AI-generated content may contain errors. Please verify critical information