The slope of the normal to the curve y = 2n² + 3 sin n at n = 0 is -
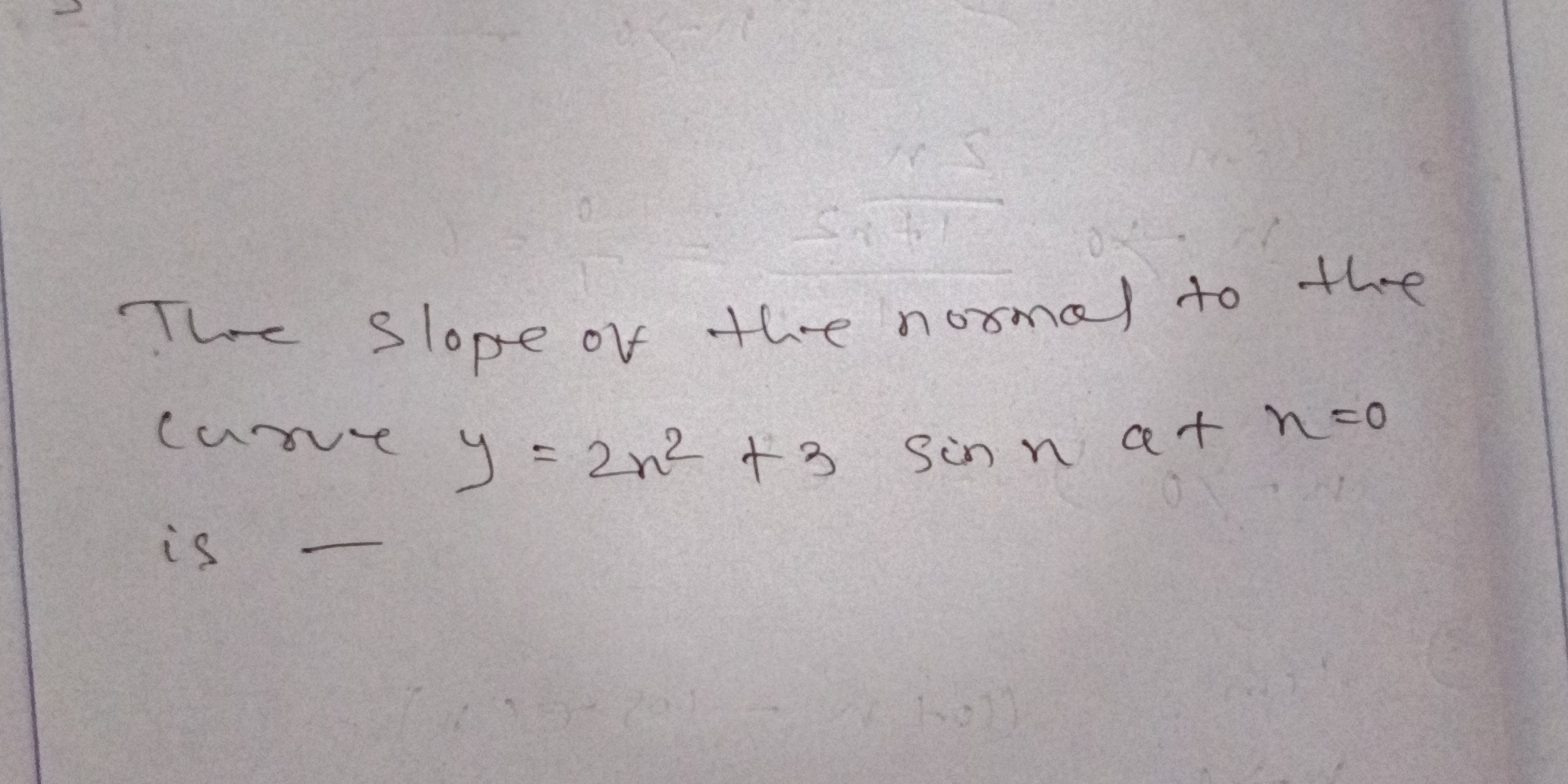
Understand the Problem
The question is asking for the slope of the normal line to the curve defined by the equation y = 2n² + 3sin(n) at the point where n = 0. To find this, we first need to compute the derivative of the curve to obtain the slope of the tangent line and then use this information to calculate the slope of the normal line.
Answer
The slope of the normal to the curve at \( n = 0 \) is $-\frac{1}{3}$.
Answer for screen readers
The slope of the normal to the curve at ( n = 0 ) is $-\frac{1}{3}$.
Steps to Solve
- Find the derivative of the function
To find the slope of the tangent line, we first need to differentiate the function $y = 2n^2 + 3\sin(n)$ with respect to $n$.
Using the power rule and the derivative of sine, we have: $$ \frac{dy}{dn} = \frac{d}{dn}(2n^2) + \frac{d}{dn}(3\sin(n)) = 4n + 3\cos(n) $$
- Evaluate the derivative at the point of interest
Next, we substitute $n = 0$ into the derivative to find the slope of the tangent line: $$ \frac{dy}{dn} \bigg|_{n=0} = 4(0) + 3\cos(0) = 0 + 3 = 3 $$
- Calculate the slope of the normal line
The slope of the normal line is the negative reciprocal of the slope of the tangent line. Therefore: $$ m_{normal} = -\frac{1}{m_{tangent}} = -\frac{1}{3} $$
The slope of the normal to the curve at ( n = 0 ) is $-\frac{1}{3}$.
More Information
The normal line is a line perpendicular to the tangent line at the point of interest. Knowing the slopes of both lines is important for understanding the behavior of curves in calculus.
Tips
- Forgetting to take the negative reciprocal when finding the slope of the normal line.
- Not substituting the correct value into the derivative, leading to an incorrect slope calculation.
AI-generated content may contain errors. Please verify critical information