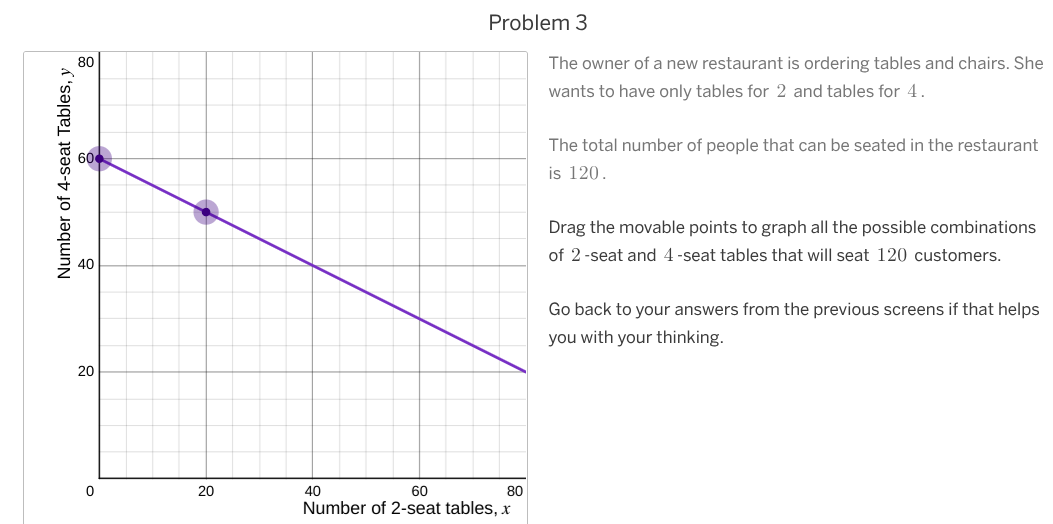
The owner of a new restaurant is ordering tables and chairs. She wants to have only tables for 2 and tables for 4. The total number of people that can be seated in the restaurant i... The owner of a new restaurant is ordering tables and chairs. She wants to have only tables for 2 and tables for 4. The total number of people that can be seated in the restaurant is 120. Drag the movable points to graph all the possible combinations of 2-seat and 4-seat tables that will seat 120 customers.
Understand the Problem
The question describes a scenario where a restaurant owner wants to order tables for 2 and 4 people. The restaurant needs to seat a total of 120 people. The question presents a graph and ask to find all possible combinations of 2-seat and 4-seat tables that will seat 120 customers.
Answer
The line passes through the points $(0, 30)$ and $(60, 0)$.
Answer for screen readers
The two points that define the line are $(0, 30)$ and $(60, 0)$.
Steps to Solve
- Define variables
Let $x$ be the number of 2-seat tables and $y$ be the number of 4-seat tables.
- Formulate the equation
The total number of people that can be seated is 120. This gives us the equation: $2x + 4y = 120$
- Find the intercepts
To find the intercepts, we can set $x = 0$ and $y = 0$ separately and solve for the other variable.
- Solve for y-intercept
When $x = 0$: $2(0) + 4y = 120$ $4y = 120$ $y = \frac{120}{4}$ $y = 30$ So, the y-intercept is $(0, 30)$.
- Solve for x-intercept
When $y = 0$: $2x + 4(0) = 120$ $2x = 120$ $x = \frac{120}{2}$ $x = 60$ So, the x-intercept is $(60, 0)$.
- Graph the line
Plot the points $(0, 30)$ and $(60, 0)$ on the graph and draw a line through them. This line represents all possible combinations of 2-seat and 4-seat tables that can seat 120 customers.
The two points that define the line are $(0, 30)$ and $(60, 0)$.
More Information
The line represents all possible combinations of 2-seat and 4-seat tables that accommodate 120 people. Any point on this line with integer coordinates represents a valid solution to the problem.
Tips
A common mistake is to miscalculate the intercepts or to plot the points incorrectly. Ensure you correctly substitute $x=0$ and $y=0$ into the equation and solve for the remaining variable. Also, double-check that you plot the points correctly on the graph.
AI-generated content may contain errors. Please verify critical information