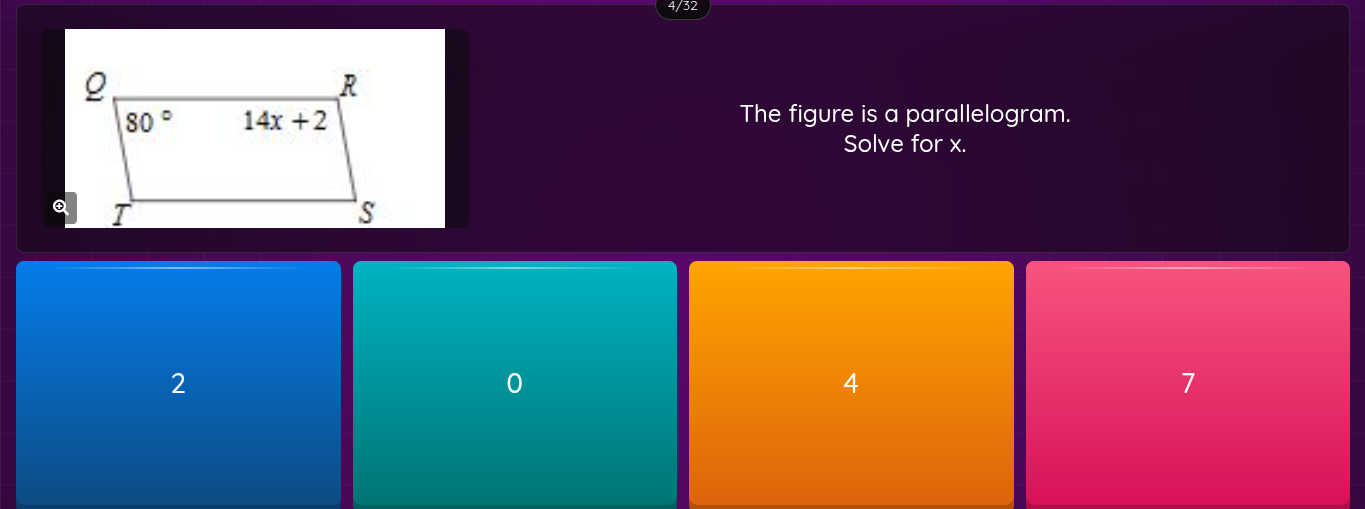
The figure is a parallelogram. Solve for x given that two angles measure 80° and 14x + 2.
Understand the Problem
The question asks us to find the value of 'x' in a parallelogram, given the measure of two angles. Since opposite angles in a parallelogram are equal, we can set up an equation to solve for 'x'. That is, 80 = 14x + 2
Answer
$x = \frac{39}{7}$
Answer for screen readers
$x = \frac{39}{7}$
Steps to Solve
- State the property of parallelograms
In a parallelogram, opposite angles are equal.
- Set up the equation
Using the given angle measures, we can set up the equation:
$14x + 2 = 80$
- Solve for x
Subtract 2 from both sides of the equation:
$14x + 2 - 2 = 80 - 2$
$14x = 78$
- Isolate x
Divide both sides by 14:
$\frac{14x}{14} = \frac{78}{14}$
$x = \frac{39}{7}$
$x = \frac{39}{7}$
More Information
The value of $x$ is $\frac{39}{7}$, which is approximately 5.57. None of the answer choices provided in the image are the correct value for $x$. It seems that choices are incorrect
Tips
A common mistake might be incorrectly setting up the equation, for example by assuming adjacent angles are equal rather than opposite angles.
AI-generated content may contain errors. Please verify critical information